Поле радиации в условиях многоярусной облачности рассматривалось во многих работах, например , , . При применении методов расчета характеристик солнечной радиации (потоков или интенсивности), развитых в этих работах возникают значительные трудности, связанные с необходимостью учета формальной взаимосвязанности всех слоев. При решении обратных задач эти трудности усугубляются. Однако при решении реальных задач, особенно касающихся облачных слоев большой оптической толщины, всей совокупностью взаимосвязей можно пренебречь и рассматривать каждый слой независимо, учитывая влияние соседних слоев приближенно. Именно такой подход был развит в работе при расчете нисходящих и восходящих потоков рассеянной солнечной радиации в вертикально неоднородной и оптически толстой среде, состоящей из двух оптически толстых слоев, с различными оптическими свойствами. При этом принималось допущение, что учет влияния верхнего слоя осуществляется путем рассмотрения потока рассеянного излучения, пропущенного этим слоем, а нижнего слоя – его сферического альбедо. Таким образом, угловое распределение поля рассеянной радиации, входящей снизу в верхний слой и сверху в нижний слой, учитывается приближенно. Проведенная оценка точности предложенного способа показала, что погрешность результатов расчета, вызванная принятым приближением, составляет менее 1%.
Пусть суммарная оптическая толщина системы n облачных слоев  = = 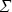  i,>>1, где i,>>1, где  i – оптические толщины отдельных подслоев. Альбедо однократного рассеяния радиации в подслоях – i – оптические толщины отдельных подслоев. Альбедо однократного рассеяния радиации в подслоях –  0i, причем 1- 0i, причем 1-  0i << 1. Объемные коэффициенты поглощения в каждом из слоев – 0i << 1. Объемные коэффициенты поглощения в каждом из слоев – 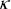 i = i =  i(1- i(1- 0i) и объемные коэффициенты рассеяния – 0i) и объемные коэффициенты рассеяния –  i = i =  i i 0i. Рассеянием радиации в оптически тонких слоях атмосферы между облачными слоями как и в подоблачном слое атмосферы будем пренебрегать и считаем, что нижний облачный слой опирается на подстилающую поверхность с альбедо A. 0i. Рассеянием радиации в оптически тонких слоях атмосферы между облачными слоями как и в подоблачном слое атмосферы будем пренебрегать и считаем, что нижний облачный слой опирается на подстилающую поверхность с альбедо A.
Потоки рассеянного излучения выходящего из оптически толстого однородного облачного слоя, выраженные в единицах падающего на слой потока pS, описываются асимптотическими формулами (2.2.3). При рассмотрении системы из нескольких слоев будем полагать, как это было предложено для двух слоев в , что справедливы формулы (2.2.3), причем в качестве альбедо A1 для верхнего слоя принимается величина:
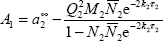
– сферическое альбедо 2-го слоя (при отсчете сверху). Величина a2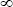 обозначает сферическое альбедо полубесконечной атмосферы со свойствами второго слоя: a2 обозначает сферическое альбедо полубесконечной атмосферы со свойствами второго слоя: a2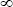 =1 - 4s2 + 6 =1 - 4s2 + 6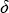 s22. Нижние индексы указывают, для какого слоя рассчитываются соответствующие величины. В системе, состоящей из n слоев, для слоя с номером i > 1 в основных формулах функция u( s22. Нижние индексы указывают, для какого слоя рассчитываются соответствующие величины. В системе, состоящей из n слоев, для слоя с номером i > 1 в основных формулах функция u(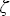 ), определенная выше, заменяется интегралом от этой функции по величине ), определенная выше, заменяется интегралом от этой функции по величине 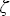 , умноженным на поток радиации, пропущенный верхним слоем: QiF , умноженным на поток радиации, пропущенный верхним слоем: QiF ( ( i-1). Введем следующие обозначения i-1). Введем следующие обозначения
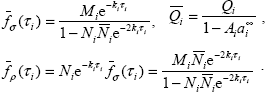 |
(2.3.1) |
Окончательно, для произвольного слоя с номером k > 1 были получены выражения для полусферических потоков рассеянной радиации на его границах :
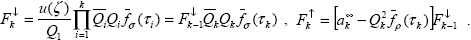 |
(2.3.2) |
При этом справедливо соотношение 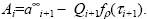
Формулы для расчета интенсивности рассеянной солнечной радиации в многослойной среде получим аналогично тому, как это было сделано выше, заменяя функцию ui(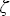 ) на произведение, описывающее входящую в рассматриваемый слой диффузную радиацию Qi ) на произведение, описывающее входящую в рассматриваемый слой диффузную радиацию Qi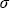 i-1( i-1( i-1, i-1,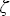 , ,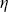 ). Выражения для интенсивности, отраженной и пропущенной подслоем с номером k, принимают вид : ). Выражения для интенсивности, отраженной и пропущенной подслоем с номером k, принимают вид :
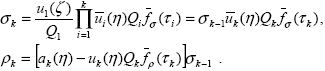 |
(2.3.3) |
В этих формулах нижние индексы у констант и функций обозначают, что они относятся к слою с соответствующим номером и оптическими параметрами gi,  0i и 0i и  i. i.
Если в i-м слое рассеяние консервативно, функция u(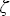 ) переходит в функцию u0( ) переходит в функцию u0(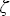 ), величины Qi и ai ), величины Qi и ai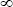 равны 1, равны 1, 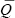 i примет значение 1/(1-Ai) и функции f i примет значение 1/(1-Ai) и функции f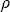 ( ( i) и f i) и f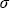 ( ( i), определяющие зависимость интенсивности от оптической толщины, выразятся формулами . i), определяющие зависимость интенсивности от оптической толщины, выразятся формулами .
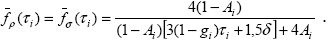 |
(2.3.4) |
Расчет потоков солнечной радиации в случае слоев произвольной оптической толщины осуществляется с использованием выражений, полученных на основе формул, приведенных в разделе 2.2 и модифицированных аналогично случаю, рассмотренному выше. Для верхнего слоя соответствующие выражения совпадают с формулами и (2.3.1):
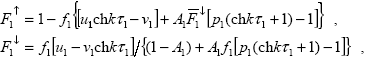 |
(2.3.5) |
где 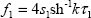 и и 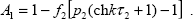
Для нижних слоев потоки на их границах выражаются формулами :
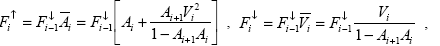 |
(2.3.6) |
где величины Ai и Vi рассчитываются, исходя из выражений
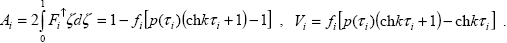 |
(2.3.7) | |