В настоящей главе выше были приведены асимптотические формулы теории переноса радиации, полученные с применением строгих математических методов. Необходимо иметь в виду, что асимптотические формулы тем точнее описывают поле радиации внутри и на границах слоя, чем больше оптическая толщина и меньше истинное поглощение, при этом наблюдается сильная зависимость точности результата от степени анизотропии рассеяния (в нашем случае от величины параметра g). Некоторые математические аспекты, связанные с оценкой области применимости асимптотических формул для коэффициентов отражения и пропускания 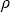 ( (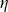 , ,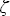 , , 0) и 0) и 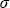 ( (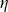 , ,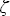 , , 0) исследованы в работах , . Точность формулы для 0) исследованы в работах , . Точность формулы для 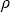 ( (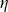 , ,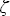 , , 0) оказалась не меньше точности формулы для 0) оказалась не меньше точности формулы для 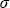 ( (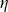 , ,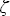 , , 0). Общий вывод таков: асимптотические формулы для отраженной и пропущенной радиации имеют погрешность ~ 2%, начиная с 0). Общий вывод таков: асимптотические формулы для отраженной и пропущенной радиации имеют погрешность ~ 2%, начиная с  0 0  4/(1 - k). Численная проверка точности формул для сферического альбедо и пропускания (значения отраженного и пропущенного потоков проинтегрированных по зенитному углу) была выполнена для широкого набора параметров в работе , где показано, что при 4/(1 - k). Численная проверка точности формул для сферического альбедо и пропускания (значения отраженного и пропущенного потоков проинтегрированных по зенитному углу) была выполнена для широкого набора параметров в работе , где показано, что при   2 и 2 и  0 0  0,7 погрешность результатов расчета интегральных по зенитному углу радиационных характеристик (сферического альбедо и интегрального пропускания) не превышает 5%. 0,7 погрешность результатов расчета интегральных по зенитному углу радиационных характеристик (сферического альбедо и интегрального пропускания) не превышает 5%.
В работе был проведен соответствующий анализ для потоков радиации, основанный на сравнении результатов расчетов с использованием асимптотических формул и метода сложения слоев. Область применимости асимптотических формул для расчета отраженного потока радиации и для лучистого притока тепла представлена на рис. 2.2 а,б. Кривые на рис. 2.2 соответствуют уровню погрешности 5%. Рассмотрены значения параметра индикатрисы рассеяния g = 0,5; 0,75 и 0,9 и два значения косинуса зенитного угла  = 1 и 0,5. Результат расчета пропущенного потока радиации подобен результату, показанному на рис. 2.2 для отраженного потока. = 1 и 0,5. Результат расчета пропущенного потока радиации подобен результату, показанному на рис. 2.2 для отраженного потока.
Численный анализ области применимости асимптотик для расчета интенсивности радиации в оптически толстом слое проведен в откуда следует, что область применимости асимптотик при расчете интенсивности ( > 15; > 15;  0 > 0,99), ограничена сильнее, чем при расчете потоков ( 0 > 0,99), ограничена сильнее, чем при расчете потоков ( > 7; > 7;  0 > 0,9), которая, в свою очередь, меньше, чем для интегральных по зенитному углу Солнца характеристик ( 0 > 0,9), которая, в свою очередь, меньше, чем для интегральных по зенитному углу Солнца характеристик ( > 2; > 2;  0 > 0,8). 0 > 0,8).
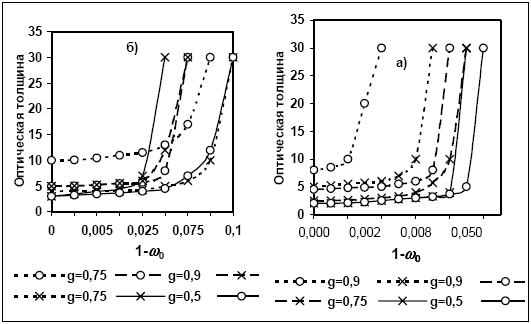
Рисунок 2.1. Область применимости асимптотических формул теории переноса излучения при расчете отраженного потока (а) и лучистого притока (б) радиации к слою. Кривые соответствуют уровню относительной ошибки 5%. Сплошная линия - параметр индикатрисы g=0,5; штриховая - g=0,75 и штрих-пунктирная линия - g=0,9; кривые, отмеченные кружками соответствуют  =1, крестиками - =1, крестиками -  =0,5. =0,5.
Таблица 2.5.
Погрешности расчета функции u(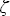 ), ),
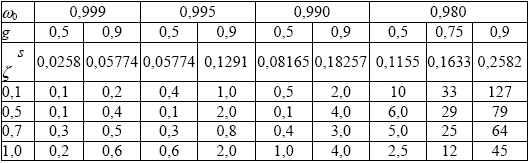
Точность асимптотических разложений (2.2.6) и (2.2.7) определяется отбрасываемыми слагаемыми в соответствующих суммах и пропорциональными s3 или s4. Точность аппроксимаций, была проверена сравнением со значениями функций, рассчитанными численными методами и представленными в , . Для функции u(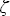 ), рассчитанной с применением аппроксимаций (2.2.8) относительные погрешности приведены в табл.2.5. Оказалось, что погрешности малы вплоть до ), рассчитанной с применением аппроксимаций (2.2.8) относительные погрешности приведены в табл.2.5. Оказалось, что погрешности малы вплоть до  0 =0,98 при слабо вытянутой индикатрисе рассеяния (g = 0,5) и z > 0,2, при этом погрешность расчета функции u( 0 =0,98 при слабо вытянутой индикатрисе рассеяния (g = 0,5) и z > 0,2, при этом погрешность расчета функции u(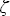 ) не превышает 6%. ) не превышает 6%.
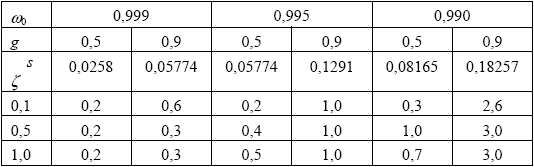
Сравнение результатов расчета 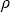 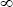 ( (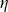 , ,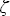 ) с учетом коэффициентов ) с учетом коэффициентов 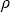 2( 2(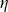 , ,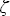 ) и ) и 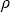 3( 3(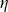 , ,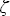 ) разложения (2.2.7), полученных выше, с результатами, полученными строгим численным методом в работе , показали погрешности приведенные в таблице 2.6. Выражения для коэффициентов ) разложения (2.2.7), полученных выше, с результатами, полученными строгим численным методом в работе , показали погрешности приведенные в таблице 2.6. Выражения для коэффициентов 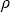 2( 2(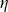 , ,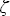 ) и ) и 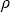 3( 3(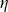 , ,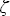 ) (2.2.8) позволяют рассчитывать соответствующие величины с малой погрешностью вплоть до значений ) (2.2.8) позволяют рассчитывать соответствующие величины с малой погрешностью вплоть до значений  0 = 0,9. Таким образом, вычисление интенсивности солнечной радиации в видимом диапазоне спектра, отраженной от облачного слоя можно проводить на основе аналитических формул, что важно при интерпретации спутниковых наблюдений. При проверке формул принимались табличные значения функции 0 = 0,9. Таким образом, вычисление интенсивности солнечной радиации в видимом диапазоне спектра, отраженной от облачного слоя можно проводить на основе аналитических формул, что важно при интерпретации спутниковых наблюдений. При проверке формул принимались табличные значения функции 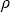 0( 0(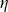 , ,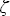 ), полученные в на основе численных методов расчета. ), полученные в на основе численных методов расчета.
Точность и область применимости формул для потоков радиации в случае слоя произвольной оптической толщины оценивались из сравнения результатов расчета потоков, выходящих из слоя произвольной оптической толщины с применением формул (2.5.1) – (2.5.3) с результатами расчетов, выполненных с использованием методов: сложения слоев, дельта-Эддингтона, и Монте-Карло. При этом был проанализирован широкий набор переменных  0 = 0,1 – 5,0; 0 = 0,1 – 5,0;  0 = 0,99 – 0,9999 и g = 0,25 – 0,75 . Оказалось, что результаты всех 4-х методов совпадают с отклонением от 0,01 до 5% не зависимо от величин 0 = 0,99 – 0,9999 и g = 0,25 – 0,75 . Оказалось, что результаты всех 4-х методов совпадают с отклонением от 0,01 до 5% не зависимо от величин  0, 0,  0 и g. Таким образом, можно полагать, что все просмотренные значения оптических параметров с погрешностью меньшей 5% попадают в область применимости формул, полученных в работах [19,20]. Для слабо вытянутой индикатрисы рассеяния (g 0 и g. Таким образом, можно полагать, что все просмотренные значения оптических параметров с погрешностью меньшей 5% попадают в область применимости формул, полученных в работах [19,20]. Для слабо вытянутой индикатрисы рассеяния (g 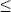 0,5) погрешность оказалась менее 1% . 0,5) погрешность оказалась менее 1% .
Точность расчета радиационных характеристик по формулам (2.3.1) – (2.3.4) для многослойной облачности была проверена для случаев  i = 5; 7; 10, gi = 0,65; 0,75; 0,85 и i = 5; 7; 10, gi = 0,65; 0,75; 0,85 и  0i = 0,99; 0,995; 0,999 сравнением с результатами расчета с помощью метода сложения слоев. Оказалось, что, если оптическая толщина подслоев удовлетворяет условию 0i = 0,99; 0,995; 0,999 сравнением с результатами расчета с помощью метода сложения слоев. Оказалось, что, если оптическая толщина подслоев удовлетворяет условию  i i  7, погрешность результатов расчета радиационных характеристик на границах слоев не превышает 1-2% для всех рассмотренных случаев, при 7, погрешность результатов расчета радиационных характеристик на границах слоев не превышает 1-2% для всех рассмотренных случаев, при  i < 5 погрешность составляет более 10%. i < 5 погрешность составляет более 10%.
Таблица 2.6.
Погрешности расчета функции 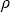  ( (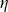 , ,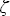 ) с применением асимптотического разложения (2.2.7) и формул (2.2.14) ) с применением асимптотического разложения (2.2.7) и формул (2.2.14)
|