Простейшей и, в то же время, важнейшей характеристикой отражения солнечного излучения от подстилающей поверхности является альбедо поверхности – отношение отраженного от нее потока излучения к падающему потоку на поверхность:
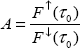 . . |
(1.4.1) |
Эта характеристика имеет наглядный физический смысл – она соответствует доле энергии приходящего на поверхность излучения, которая отражается обратно. Действительно, если A=0, то поверхность полностью поглощает все излучение (абсолютно черная поверхность), если A=1, то, наоборот, поверхность ничего не поглощает, а целиком отражает излучение (абсолютно белая поверхность). Обобщая понятие альбедо, вводят альбедо системы «атмосфера плюс поверхность», определяя его как аналогичное (1.4.1) отношение потоков на произвольном уровне 
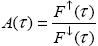 . . |
(1.4.2) |
Напомним, что всюду здесь речь идет о величинах, определенных для одной длины волны, т.е. спектральных характеристиках поля излучения и поверхности. В энергетике атмосферы важную роль играет интегральное альбедо, которое нередко для краткости называют просто “альбедо”. Его не следует путать с рассматриваемым спектральным альбедо.1
Альбедо поверхности характеризует процесс отражения излучения лишь с точки зрения описания трансформации энергии, однако, ничего не говорит о зависимости интенсивности отраженного излучения от угла и азимута отражения. Если бы поверхность была идеально плоской, то такая зависимость определялась бы хорошо известными законами отражения и преломления . Однако все реальные природные поверхности являются шероховатыми, т.е. содержат неровности различных масштабов, и даже водная поверхность практически всегда не является гладкой. Поэтому, при рассмотрении отражения падающего на поверхность параллельного пучка лучей, несмотря на то, что отражение от каждой микро-неровности подчиняется “классическим” законам, в совокупности получается более сложная картина. В частности, отраженное излучение распространяется во всех возможных направлениях, а не только в направлении, соответствующем закону “угол отражения равен углу падения”. Такое отражение света от реальных поверхностей принято называть диффузным.
Можно выделить три основных типа диффузного отражения: ортотропное (или изотропное) отражение, когда интенсивность диффузно отраженного излучения не зависит от направления; зеркальное отражение, когда максимум интенсивности отраженного излучения находится в направлении угла зеркального отражения (т.е. угла, равного углу падения), и обратное отражение, когда максимум находится в направлении, противоположном направлению падающего излучения. Заметим, что зеркальное отражение характерно для поверхностей, близких к идеально плоским, что понятно, а обратное, наоборот, – для сильно шероховатых поверхностей, поскольку, очевидно, вызывается наличием значительного числа микроплощадок, ориентированных перпендикулярно падающему свету. Экспериментальные измерения, некоторые из которых мы подробнее рассмотрим в гл. 3, показывают, что наиболее близки к ортотропным поверхностям снег и облака (если условно считать облака за “поверхность”), самая зеркальная поверхность – вода, а остальные поверхности в основном обратно отражающие. Впрочем, ссылка на измерения тут даже излишняя, поскольку зеркальное отражение берегов от воды видели все, а максимум обратного отражения очень четко визуально наблюдается с самолета.
Ортотропные поверхности занимают некое особое положение, поскольку все их отражательные характеристики сводятся к единственной скалярной величине – альбедо. По этой причине и по простоте математического описания процессов отражения от них, ортотропные поверхности очень часто используются при теоретическом анализе и численных расчетах поля излучения. Заметим, однако, что, как и всякая идеализация, предположение об ортотропности отражения является приближением, точность которого следует оценивать при решении конкретных задач. Для прочих поверхностей говорят об анизотропии отражения, которая очевидно требует для своего описания дополнительных понятий. Рассматривают достаточно разнообразные характеристики отражения от анизотропных поверхностей, однако здесь мы опишем проблему учета отражения в общем виде, не прибегая к излишней конкретизации. Отметим, что процессы отражения зависят от поляризации падающего излучения и сопровождаются изменением этой поляризации . Поэтому рассмотрение отражения без учета поляризации есть приближение. Учитывая, однако, различную ориентацию микро-неровностей реальных поверхностей, можно утверждать, что чем ближе отражение к ортотропному, тем менее поляризованным будет отраженное излучение (равномерное распределение отраженного излучения по направлениям соответствует чисто хаотической ориентации микро-отражателей, что, в свою очередь, дает хаотическое распределение эллипсов поляризации, т.е. неполяризованный свет). Таким образом, ортотропность отражения одновременно означает и отсутствие его зависимости от поляризации. И наоборот, чем сильнее анизотропия, тем более эта зависимость может проявляться. Наиболее анизотропной является водная поверхность, поэтому при рассмотрении отражения от нее вопрос о точности приближения неполяризованного излучения, вообще говоря, требует отдельного изучения.
В общем случае отражение излучения от поверхности можно характеризовать функцией R( , , , , ', ', '), определяемой из соотношения между интенсивностями I( '), определяемой из соотношения между интенсивностями I( 0, 0, ', ', , , ') падающего на поверхность ( ') падающего на поверхность ( ' > 0) и I( ' > 0) и I( 0, 0, , , , , ) отраженного от поверхности ( ) отраженного от поверхности ( < 0)) излучения < 0)) излучения
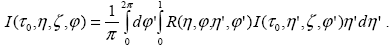 . . |
(1.4.3) |
Легко проверить, что для ортотропной поверхности выражения (1.4.3) и (1.4.1) дают R( , , , , ', ', ')=A, именно из соображений такой “нормировки” в (1.4.3) и введен множитель ')=A, именно из соображений такой “нормировки” в (1.4.3) и введен множитель  '/ '/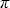 , в принципе его присутствие не обязательно. В операторной форме выражение (1.4.3) запишется в виде : , в принципе его присутствие не обязательно. В операторной форме выражение (1.4.3) запишется в виде :
I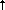 =RI =RI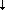 , , |
(1.4.4) |
где I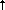 =I( =I( 0, 0, , , , , ) – интенсивность отраженного излучения, I ) – интенсивность отраженного излучения, I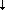 = I( = I( 0, 0, , , , , ) – интенсивность падающего излучения, – оператор отражения от поверхности. ) – интенсивность падающего излучения, – оператор отражения от поверхности.
Идея учета отражения от поверхности в теории переноса излучения основана на очевидном утверждении, что отражение эквивалентно освещению атмосферы снизу (т.е. со стороны нижней границы атмосферы  = =  0). Таким образом, достаточно уметь решать задачу переноса исключительно для рассеянного в атмосфере излучения, причем как при освещении сверху, так и при освещении снизу, а затем “добавить” отраженное от поверхности излучение на основе полученных решений. 0). Таким образом, достаточно уметь решать задачу переноса исключительно для рассеянного в атмосфере излучения, причем как при освещении сверху, так и при освещении снизу, а затем “добавить” отраженное от поверхности излучение на основе полученных решений.
Введем, согласно , следующую систему обозначений. Величины, относящиеся к системе “атмосфера плюс поверхность” будем отмечать верхней чертой, величины, относящиеся к атмосфере без учета поверхности при освещении снизу, – тильдой, а относящиеся к атмосфере без учета поверхности при освещении сверху, будем, как и раньше, использовать без специальных отметок. Тогда решение задачи переноса при освещении сверху в операторном виде (1.3.26) запишется как I = TI0, где I0 – интенсивность солнечного излучения на верхней границе. Для интенсивности излучения на нижней границе атмосферы I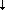 введем соответствующий оператор T введем соответствующий оператор T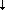 , так что I , так что I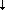 = T = T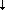 I0, причем подчеркнем, что T I0, причем подчеркнем, что T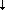 должен описывать перенос и рассеянного, и прямого солнечного излучения. Последнее мы исключили из уравнения переноса, а потому обязаны специально учесть при отражении от поверхности. Решение задачи переноса при освещении снизу запишется как должен описывать перенос и рассеянного, и прямого солнечного излучения. Последнее мы исключили из уравнения переноса, а потому обязаны специально учесть при отражении от поверхности. Решение задачи переноса при освещении снизу запишется как 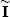 = =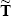 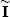 1, где 1, где 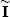 1 описывает поле излучения, приходящее снизу на нижнюю границу, которое учитывается согласно формуле (1.3.27), при этом, по указанным выше причинам, оператор 1 описывает поле излучения, приходящее снизу на нижнюю границу, которое учитывается согласно формуле (1.3.27), при этом, по указанным выше причинам, оператор 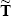 должен описывать и перенос прямого отраженного излучения (т.е. идущего от поверхности без рассеяния). Для интенсивности излучения, приходящего сверху на нижнюю границу, освещаемую снизу излучением с интенсивностью должен описывать и перенос прямого отраженного излучения (т.е. идущего от поверхности без рассеяния). Для интенсивности излучения, приходящего сверху на нижнюю границу, освещаемую снизу излучением с интенсивностью 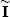 1, введем оператор 1, введем оператор 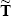 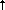 , так что , так что 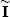 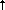 = =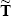 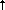 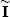 1. По смыслу величина 1. По смыслу величина 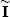 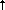 – это интенсивность излучения вновь приходящего на поверхность сверху в результате рассеяния в атмосфере излучения, отраженного от подстилающей поверхности. Заметим, что как следует из предыдущего параграфа, математически задача построения всех искомых операторов T, T – это интенсивность излучения вновь приходящего на поверхность сверху в результате рассеяния в атмосфере излучения, отраженного от подстилающей поверхности. Заметим, что как следует из предыдущего параграфа, математически задача построения всех искомых операторов T, T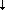 , , 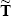 , ,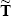 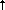 единообразна. единообразна.
Интенсивность при учете отражения от поверхности, очевидно, может быть получена как сумма следующих составляющих. Во-первых, это интенсивность рассеянного в атмосфере прямого солнечного излучения TI0. Во-вторых, – интенсивность прямого и рассеянного в атмосфере отраженного излучения 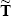 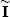 1, что с учетом (1.4.4) есть 1, что с учетом (1.4.4) есть 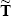 RT RT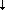 I0. Далее следует учет вторично отраженного излучения I0. Далее следует учет вторично отраженного излучения 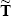 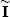 2 = 2 = 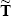 (R (R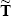 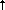 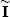 1) = 1) = 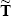 (R (R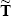 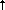 RT RT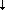 I0) и т.д. В итоге для величины искомой интенсивности получаем . I0) и т.д. В итоге для величины искомой интенсивности получаем .
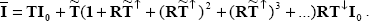 |
(1.4.5) |
Выражение (1.4.5) известно как разложение интенсивности излучения в ряд по кратности отражения. Оно очень широко используется в схемах численного решения задач, где позволяет легко организовать рекуррентные вычисления искомой интенсивности. Заметим, что ряд (1.4.5) сходится тем быстрее, чем слабее отражение. Операторный подход представлен, в частности, в монографиях , .
Рассмотрим теперь одну частную задачу, связанную с переносом излучения и с учетом отражающей поверхности. Пусть нас интересует интенсивность излучения не во всей атмосфере, а лишь на границах ее, т.е. 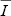 (0, (0, , , , , ) ( ) ( <0) и <0) и 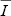 ( ( 0, 0, , , , , ) ( ) ( >0). Очевидные примеры – это задачи, связанные с интерпретацией спутниковых и наземных измерений интенсивности рассеянного солнечного излучения. В подобных задачах, для удобства, все углы, под которыми выходит излучение из атмосферы, принято измерять в интервале [0, >0). Очевидные примеры – это задачи, связанные с интерпретацией спутниковых и наземных измерений интенсивности рассеянного солнечного излучения. В подобных задачах, для удобства, все углы, под которыми выходит излучение из атмосферы, принято измерять в интервале [0,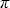 /2], т.е. все значения /2], т.е. все значения  считать положительными. Для согласования этих стандартов с рассматриваемой геометрией переноса излучения (рис. 1.3.2), искомые величины интенсивности запишутся как считать положительными. Для согласования этих стандартов с рассматриваемой геометрией переноса излучения (рис. 1.3.2), искомые величины интенсивности запишутся как 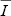 (0,- (0,- , , , , ) и ) и 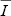 ( ( 0, 0, , , , , ) (заметим, что ) (заметим, что  рассматривается как независимая переменная, поэтому в любых случаях рассматривается как независимая переменная, поэтому в любых случаях  > 0). > 0).
Введем по [2] коэффициенты яркости атмосферы, определяемые из соотношений
I(0,-  , , , , ) = S ) = S ( ( , , , , ), I(0,- ), I(0,- , , , , ) = S ) = S ( ( , , , , ), ), |
(1.4.6) |
где 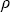 ( ( , , , , ) – коэффициент диффузного отражения атмосферы, ) – коэффициент диффузного отражения атмосферы, 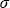 ( ( , , , , ) – коэффициент диффузного пропускания атмосферы (напомним систему обозначений – без учета поверхности). Введем аналогичные коэффициенты для случая освещения снизу ) – коэффициент диффузного пропускания атмосферы (напомним систему обозначений – без учета поверхности). Введем аналогичные коэффициенты для случая освещения снизу
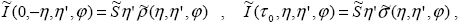 |
(1.4.7) |
определив их для направления падения параллельного потока излучения 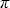 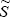 на нижнюю границу атмосферы ( на нижнюю границу атмосферы ( ',0), причем “перевернутую” геометрию условимся считать полностью аналогичной случаю освещения атмосферы сверху, поэтому ',0), причем “перевернутую” геометрию условимся считать полностью аналогичной случаю освещения атмосферы сверху, поэтому  ' > 0, – это верхняя граница атмосферы и т.д. Важнейшими свойствами коэффициентов яркости являются соотношения симметрии. ' > 0, – это верхняя граница атмосферы и т.д. Важнейшими свойствами коэффициентов яркости являются соотношения симметрии.
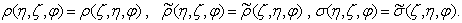 |
(1.4.8) |
Доказательство соотношений (1.4.8) в общем случае не является элементарным, оно приведено, например, в монографии . Введем определения, аналогичные (1.4.6), для коэффициентов яркости системы “атмосфера плюс поверхность” 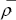 ( ( , , , , ) и ) и 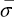 ( ( , , , , ). ).
Для коэффициентов яркости можно избавиться от азимутальной зависимости, если искать их в виде разложения по азимутальным гармоникам
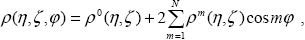 |
(1.4.9) |
(и аналогичные разложения для 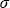 ( ( , , , , ), ), 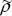 ( ( , , , , ), и т.д.), при этом очевидно для каждой гармоники выполняются соотношения симметрии (1.4.8) ( ), и т.д.), при этом очевидно для каждой гармоники выполняются соотношения симметрии (1.4.8) (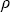 m( m( , , ,) = ,) = 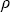 m( m( , , ) и т.д.). ) и т.д.).
Рассмотрим простейший, но часто встречающийся случай ортотропной поверхности с альбедо, равным A. Легко показать , что при изотропном отражении достаточно рассмотреть лишь нулевые гармоники коэффициентов яркости. Действительно, если бы при учете отраженного излучения менялись ненулевые гармоники (1.4.9), это бы, согласно определениям (1.4.6) – (1.4.7) означало зависимость интенсивности отраженного излучения от азимута, что противоречит предположению об ортотропности отражения.
Выпишем для данной задачи явный вид интегральных операторов из выражения (1.4.5). Согласно определению оператора T (1.3.27) и выражению для внеатмосферной интенсивности I0 (1.3.10), имеем
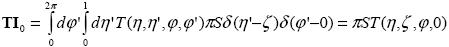 , ,
откуда, сравнивая с определением коэффициентов яркости (1.4.6) и учитывая только нулевые гармоники, получаем
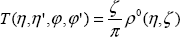 для верхней границы атмосферы для верхней границы атмосферы
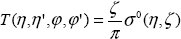 для нижней границы атмосферы (здесь для нижней границы атмосферы (здесь  ' '   и и  ' '  0). 0).
Для описания отражения от поверхности, как мы отмечали выше, надо учесть еще прямое излучение, поэтому
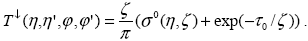
Для случая освещения снизу с направления ( ' ' ') получим, очевидно, аналогичные выражения, а далее, согласно определению оператора (1.3.27) и с учетом того, что в силу ортотропности отражения ') получим, очевидно, аналогичные выражения, а далее, согласно определению оператора (1.3.27) и с учетом того, что в силу ортотропности отражения 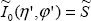 , что следует из связи потока и интенсивности (1.1.4) и равенства потока в определениях (1.4.7) , что следует из связи потока и интенсивности (1.1.4) и равенства потока в определениях (1.4.7) 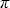 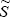 , окончательно получаем , окончательно получаем
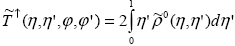
для нижней границы атмосферы, т.е. реально 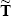 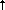 зависит только от зависит только от  . Аналогично имеем выражение: . Аналогично имеем выражение:
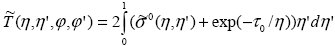
для верхней границы, где учтено прямое излучение, и условие 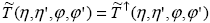 для нижней границы. для нижней границы.
Далее находим согласно определениям (1.3.27) и (1.4.3) произведение интегральных операторов
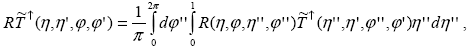
что, при подстановке полученных выше выражений, в частности R = A, дает для константу AC, где
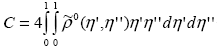 . . |
(1.4.10) |
Совершенно аналогично находим R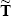 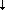 как A как A 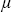 ( ( ), где ), где
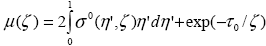 . . |
(1.4.11) |
Поскольку есть константа по отношению к переменным интегрирования, то, с учетом соотношения симметрии (1.4.8), получаем для верхней границы, для нижней границы, где
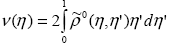 . . |
(1.4.12) |
Теперь, подставляя полученные выражения в ряд (1.4.5), суммируя получающуюся геометрическую прогрессию и учитывая определения коэффициентов яркости (1.4.6) и разложения (1.4.9), приходим к известным соотношениям
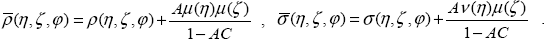 |
(1.4.13) |
Соотношения (1.4.13) с учетом (1.4.10) – (1.4.12) выражают простую связь между коэффициентами яркости системы “атмосфера плюс ортотропная поверхность” и коэффициентами яркости атмосферы без учета отражения от поверхности. Таким образом, учет поверхности в данном случае является действительно несложной задачей. Заметим, что симметрия коэффициента диффузного отражения сохраняется и при наличии отражения от подстилающей поверхности 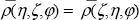 . .
1Необходимо подчеркнуть, что формально альбедо, как и прочие характеристики отражения, определяется только для поверхности, без атмосферы. В теории переноса их часто называют “истинными”. При учете наличия атмосферы получаются, строго говоря, другие аналогично определенные характеристики системы “атмосфера плюс поверхность”. Так, например, падающий на поверхность поток при наличии рассеивающей атмосферы сам зависит от альбедо поверхности (истинного), поскольку содержит долю отраженного излучения, затем вновь рассеянного в направлении к поверхности. Заметим, что в формулах теории переноса для характеристик отражения поверхности всегда используются истинные величины, в то время как непосредственному измерению всегда доступны лишь отражательные характеристики системы “атмосфера плюс поверхность”. |