Рассмотрим некоторую условную частицу вещества (молекулу газа, аэрозольную частицу), освещенную параллельным пучком лучей с потоком F0 (рис.1.4). Процесс взаимодействия излучения с данной частицей складывается из рассеяния излучения на частице и поглощения излучения веществом частицы. В сумме эти процессы называются ослаблением излучения (название связано с тем, что если рассматривать излучение в направлении распространения исходного пучка за частицей, то процессы рассеяния и поглощения приводят к уменьшению потока излучения). Пусть энергия поглощенного излучения равна Ea (a - absorption), рассеянного (во всех направлениях) – Es (s - scattering) и, соответственно, энергия ослабления Ee = Ea + Es (e – extinction). Если бы частица взаимодействовала с излучением по законам геометрической оптики и была непрозрачной (т.е. ослабляла все падающее на нее излучение), то, очевидно, энергия ослабления соответствовала бы энергии, приходящей на проекцию частицы на плоскость, перпендикулярную направлению распространения лучей . По-другому, эта проекция называется сечением частицы указанной плоскостью, ее площадь для краткости именуют просто сечением. Тогда, измеряя энергию ослабления dEe в спектральном интервале [ , ,  + d + d ] и временном интервале [t, t + dt], мы бы согласно определению потока (1.1.3) нашли сечение ослабления как ] и временном интервале [t, t + dt], мы бы согласно определению потока (1.1.3) нашли сечение ослабления как 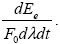
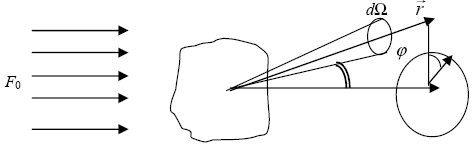
Рисунок 1.1. К определению сечений взаимодействия.
Однако реально, в силу волновой и квантовой природы света, взаимодействие его с веществом не подчиняется законам геометрической оптики. Тем не менее, оказывается очень удобным все-таки ввести отношение 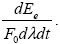 , имеющее размерность и смысл площади, понимая его в контексте эквивалентности энергии реального взаимодействия и энергии взаимодействия с непрозрачной частицей сечения , имеющее размерность и смысл площади, понимая его в контексте эквивалентности энергии реального взаимодействия и энергии взаимодействия с непрозрачной частицей сечения 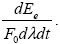 по законам геометрической оптики. Кроме того, удобно также отдельно рассматривать подобные сечения для различных процессов взаимодействия. Таким образом, по определению, сечением поглощения Сa называется отношение энергии поглощения dEa, измеренной в интервалах [ по законам геометрической оптики. Кроме того, удобно также отдельно рассматривать подобные сечения для различных процессов взаимодействия. Таким образом, по определению, сечением поглощения Сa называется отношение энергии поглощения dEa, измеренной в интервалах [ , ,  + d + d ] [t, t + dt], к исходному потоку излучения F0, сечением рассеяния Cs – отношение энергии рассеяния dEs к исходному потоку и сечением ослабления Ce – отношение энергии ослабления dEe к исходному потоку: ] [t, t + dt], к исходному потоку излучения F0, сечением рассеяния Cs – отношение энергии рассеяния dEs к исходному потоку и сечением ослабления Ce – отношение энергии ослабления dEe к исходному потоку:
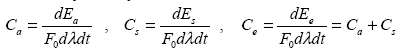 |
(1.2.1) |
При этом сечения определяются как монохроматические на длине волны  (для нестационарного случая – в момент времени t). (для нестационарного случая – в момент времени t).
Рассмотрим процесс рассеяния света частицей в некотором направлении 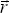 (рис.1.4.). Здесь dEd( (рис.1.4.). Здесь dEd(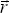 )– энергия рассеянного излучения (в интервалах [ )– энергия рассеянного излучения (в интервалах [ , ,  + d + d ], [t, t + dt]) в телесном угле d ], [t, t + dt]) в телесном угле d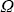 , описанным вокруг направления , описанным вокруг направления 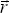 . Определим, по аналогии с сечением рассеяния, выражающимся формулой (1.2.1), сечение направленного рассеяния . Определим, по аналогии с сечением рассеяния, выражающимся формулой (1.2.1), сечение направленного рассеяния
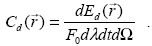 |
(1.2.2) |
Сечению Cd(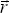 ) соответствует длина волны ) соответствует длина волны  и момент времени t. и момент времени t.
Полная энергия рассеяния, очевидно, есть интеграл от dEd(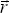 ) по всем направлениям ) по всем направлениям 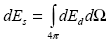 . Подставляя в этот интеграл dEd( . Подставляя в этот интеграл dEd(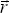 ), входящий в формулу (1.2.2) с учетом соотношения (1.2.1) получаем связь сечений рассеяния и направленного рассеяния . ), входящий в формулу (1.2.2) с учетом соотношения (1.2.1) получаем связь сечений рассеяния и направленного рассеяния .
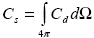 . . |
(1.2.3) |
Переходя, как и в разделе 1.1, к сферическим координатам, а именно, вводя угол рассеяния  , который определим как угол между направлениями исходного и рассеянного излучения ( , который определим как угол между направлениями исходного и рассеянного излучения (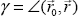 ), и азимут рассеяния ), и азимут рассеяния 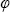 , отсчитываемый между проекцией вектора на плоскость, перпендикулярную , отсчитываемый между проекцией вектора на плоскость, перпендикулярную 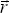 0, и некоторым (произвольно) выбранным направлением на этой плоскости, перепишем (1.2.3) в виде 1 . 0, и некоторым (произвольно) выбранным направлением на этой плоскости, перепишем (1.2.3) в виде 1 .
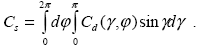 |
(1.2.4) |
Сечение направленного рассеяния, как следует из его определения, можно трактовать в том смысле, что чем больше величина Cd( , ,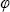 ), тем сильнее свет рассеивается именно в направлении ( ), тем сильнее свет рассеивается именно в направлении ( , ,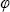 ) по сравнению с другими направлениями. Для того, чтобы можно было сравнивать сечения направленного рассеяния различных частиц, необходимо перейти к некоторой безразмерной величине, для чего следует нормировать Cd( ) по сравнению с другими направлениями. Для того, чтобы можно было сравнивать сечения направленного рассеяния различных частиц, необходимо перейти к некоторой безразмерной величине, для чего следует нормировать Cd( , ,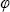 ) на интеграл Cs, выраженный соотношением (1.2.4), а также умножить результат на некоторый телесный угол. Полученная безразмерная характеристика называется индикатрисой рассеяния x( ) на интеграл Cs, выраженный соотношением (1.2.4), а также умножить результат на некоторый телесный угол. Полученная безразмерная характеристика называется индикатрисой рассеяния x( , ,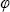 ) и определяется соотношением . ) и определяется соотношением .
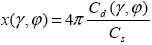 |
(1.2.5) |
Подстановка Cd( , ,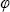 ) из (1.2.5) в (1.2.4) дает условие нормировки индикатрисы рассеяния . ) из (1.2.5) в (1.2.4) дает условие нормировки индикатрисы рассеяния .
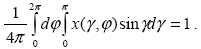 |
(1.2.6) |
Если рассеяние одинаково по всем направлениям, т.е. Cd( , ,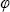 ) = const (такое рассеяние называется изотропным), то из нормировки (1.2.6) получаем x( ) = const (такое рассеяние называется изотропным), то из нормировки (1.2.6) получаем x( , ,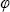 ) )  1. Из этого соображения и выбирается множитель 4 1. Из этого соображения и выбирается множитель 4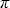 в определении индикатрисы (1.2.5). Во многих случаях (молекулярное рассеяние, рассеяние на сферических аэрозольных частицах) индикатриса не зависит от азимута рассеяния. В дальнейшем мы будем рассматривать только такие индикатрисы. Для этого случая условие нормировки (1.2.6) переходит в . в определении индикатрисы (1.2.5). Во многих случаях (молекулярное рассеяние, рассеяние на сферических аэрозольных частицах) индикатриса не зависит от азимута рассеяния. В дальнейшем мы будем рассматривать только такие индикатрисы. Для этого случая условие нормировки (1.2.6) переходит в .
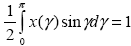 . . |
(1.2.7) |
Интеграл от индикатрисы в интервале от нуля до некоторого угла рассеяния  , т.е. , т.е. 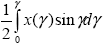 , можно трактовать как вероятность рассеяния в интервале углов от 0 до , можно трактовать как вероятность рассеяния в интервале углов от 0 до  . Легко проверить, что этот интеграл удовлетворяет всем требованиям, предъявляемым к понятию “вероятность”. Но в таком случае индикатриса рассеяния x( . Легко проверить, что этот интеграл удовлетворяет всем требованиям, предъявляемым к понятию “вероятность”. Но в таком случае индикатриса рассеяния x( ) есть плотность вероятности рассеяния излучения на угол ) есть плотность вероятности рассеяния излучения на угол  . Часто это утверждение принимают за определение индикатрисы рассеяния.2 В реальной атмосфере содержатся разнообразные частицы, с которыми взаимодействует солнечное излучение: молекулы атмосферных газов, аэрозольные частицы разного размера, формы и химического состава. Поэтому, в конечном счете, нас интересует взаимодействие не с отдельными частицами, а со всей их совокупностью в целом. Для облегчения описания такого взаимодействия со средой сложного состава в теории переноса излучения и в оптике атмосферы принято абстрагироваться от взаимодействия излучения с отдельными частицами и рассматривать атмосферу как непрерывную среду, каждому объему которой (формально сколь угодно малому объему) можно приписать определенные характеристики ее взаимодействия с излучением. . Часто это утверждение принимают за определение индикатрисы рассеяния.2 В реальной атмосфере содержатся разнообразные частицы, с которыми взаимодействует солнечное излучение: молекулы атмосферных газов, аэрозольные частицы разного размера, формы и химического состава. Поэтому, в конечном счете, нас интересует взаимодействие не с отдельными частицами, а со всей их совокупностью в целом. Для облегчения описания такого взаимодействия со средой сложного состава в теории переноса излучения и в оптике атмосферы принято абстрагироваться от взаимодействия излучения с отдельными частицами и рассматривать атмосферу как непрерывную среду, каждому объему которой (формально сколь угодно малому объему) можно приписать определенные характеристики ее взаимодействия с излучением.
Рассмотрим элементарный объем такой непрерывной среды dV = dSdl (рис.1.5.), на который перпендикулярно грани dS приходит параллельный пучок излучения с потоком F0. Взаимодействие излучения с элементарным объемом вновь сведется к процессам рассеяния и поглощения, что в сумме даст ослабление излучения после прохождения им элементарного объема. Обозначим поток излучения после прохождения элементарного объема (в направлении исходного ) как F = F0– dF. В качестве характеристики ослабления рассмотрим относительное изменение энергии падающей радиации : .
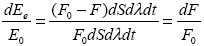
.
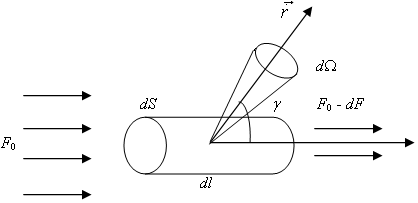
Рисунок 1.5. Взаимодействие излучения с элементарным объемом.
Поскольку оно, очевидно, пропорционально длине пути в ослабляющей среде dl, в качестве характеристики ослабления излучения элементарным объемом среды введем объемный коэффициент ослабления  , равный, по определению, относительному изменению энергии исходного излучения (измеренной в интервалах [ , равный, по определению, относительному изменению энергии исходного излучения (измеренной в интервалах [ , ,  +d +d ], [t, t + dt]), нормированному на длину dl (т.е. приведенному к единичной длине) . ], [t, t + dt]), нормированному на длину dl (т.е. приведенному к единичной длине) .
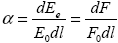 . . |
(1.2.8) |
Из равенства энергии ослабления сумме энергий поглощения и рассеяния сразу же следуют аналогичные определения для объемного коэффициента рассеяния  и объемного коэффициента поглощения и объемного коэффициента поглощения  3 , 3 ,
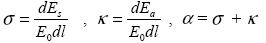 . . |
(1.2.9) |
Рассматривая энергию dEd(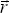 ), рассеянную в направлении ), рассеянную в направлении 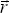 в телесном угле d в телесном угле d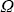 , можно было бы далее ввести “объемный коэффициент направленного рассеяния” s( , можно было бы далее ввести “объемный коэффициент направленного рассеяния” s(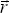 ), определив его по аналогии с (1.2.9) как ), определив его по аналогии с (1.2.9) как 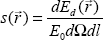 , однако подобной характеристикой для элементарного объема пользоваться не принято. Действительно, учитывая определения (1.2.9), получаем dEd( , однако подобной характеристикой для элементарного объема пользоваться не принято. Действительно, учитывая определения (1.2.9), получаем dEd(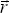 )=s( )=s(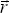 )dEsd )dEsd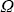 / /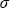 , что при подстановке в дает , что при подстановке в дает 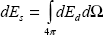 . Но это в точности соответствует нормировочному соотношению для индикатрисы рассеяния (1.2.6), если перейти к сферическим координатам (рис. 1.4 и 1.5) и положить s( . Но это в точности соответствует нормировочному соотношению для индикатрисы рассеяния (1.2.6), если перейти к сферическим координатам (рис. 1.4 и 1.5) и положить s( , ,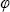 )= )=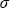 x( x( , ,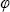 )/(4 )/(4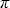 ), где x( ), где x( , ,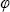 ) – индикатриса рассеяния элементарного объема. Далее, как договаривались, будем рассматривать индикатрисы рассеяния, зависящие только от угла рассеяния ) – индикатриса рассеяния элементарного объема. Далее, как договаривались, будем рассматривать индикатрисы рассеяния, зависящие только от угла рассеяния  с нормировкой (1.2.7). с нормировкой (1.2.7).
Таким образом, для энергии рассеяния в направлении  получаем соотношение . получаем соотношение .
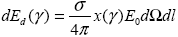 . . |
(1.2.10) |
Это соотношение можно принять за определение индикатрисы рассеяния элементарного объема среды x( ) (однако, в силу его формальности часто пользуются определением индикатрисы как плотности вероятности рассеяния на угол ) (однако, в силу его формальности часто пользуются определением индикатрисы как плотности вероятности рассеяния на угол  ). ).
Свяжем теперь характеристики взаимодействия излучения с отдельной частицей и с элементарным объемом. Пусть каждая частица взаимодействует с излучением независимо от других. Тогда энергия ослабления элементарного объема будет равна сумме энергий ослабления всех составляющих его частиц. Предположим для начала, что все частицы одинаковы, имеют сечения ослабления Ce и их счетная концентрация – число частиц в единице объема – равна n. Число частиц в элементарном объеме есть ndV, подставляя сумму энергий ослабления согласно формуле (1.2.1) в определение объемного коэффициента ослабления (1.2.8) с учетом определения потока излучения (1.1.3), получаем
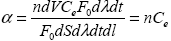 . .
Таким образом, объемный коэффициент ослабления равен произведению счетной концентрации частиц на сечение ослабления одной частицы.4
Если в элементарном объеме среды присутствуют ослабляющие частицы M сортов с концентрациями ni и сечениями Ce,i, то
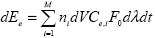 . .
Рассматривая совершенно аналогично энергии рассеяния, поглощения и направленного рассеяния, получаем формулы связи объемных коэффициентов и сечений взаимодействия .
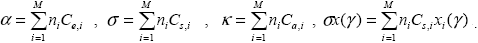 |
(1.2.11) |
Заметим, что отдельные слагаемые в (1.2.11) сами имеют смысл объемных коэффициентов взаимодействия для отдельных сортов частиц. Таким образом, из (1.2.11) непосредственно вытекают весьма важные для практических задач “правила сложения”, позволяющие находить отдельно объемные коэффициенты взаимодействия и индикатрисы рассеяния для каждой из M компонентов, а затем вычислять общие характеристики элементарного объема по формулам .
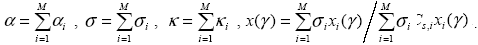 |
(1.2.12) |
В частности стандартным приемом является отдельный расчет характеристик молекулярного и аэрозольного рассеяния и поглощения излучения в атмосфере, тогда (1.2.12) переходят в соотношения .
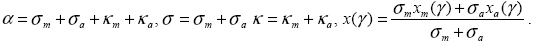 |
(1.2.13) |
где 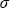 m, m, 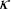 m, xm( m, xm( ) – соответственно объемные коэффициенты молекулярного рассеяния, поглощения и молекулярная индикатриса рассеяния атмосферных газов и ) – соответственно объемные коэффициенты молекулярного рассеяния, поглощения и молекулярная индикатриса рассеяния атмосферных газов и 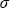 a, a, 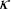 a, xa( a, xa( )‑аналогичные аэрозольные характеристики. )‑аналогичные аэрозольные характеристики.
Правила сложения, выражаемые формулами (1.2.11) ‑ (1.2.13) были получены в предположении о том, что частицы взаимодействуют с излучением независимо друг от друга. Уместен вопрос: насколько справедливо это предположение? С точки зрения геометрической оптики, апеллируя к которой мы вводили сечения взаимодействия, указанные площади (сечения) не должны перекрывать друг друга внутри элементарного объема, т.е. суммарная площадь их проекций на грань dS должна быть равна сумме площадей всех частиц. Это будет с высокой точностью выполняться, если расстояния между частицами много больше линейных размеров их сечений взаимодействия, т.е., огрубляя, много больше размеров частиц. Разбивая элементарный объем среды на кубики с гранью d, где d – характерный размер частицы, заключаем, что для выполнения этого условия число частиц в объеме dV должно быть много меньше числа указанных кубиков – ndV << dV/d3, т.е. n<<1/d3, где n ‑ счетная концентрация частиц. Второе условие независимости взаимодействия солнечного излучения с частицами среды вытекает из положений волновой оптики, согласно которой независимость взаимодействия имеет место, если расстояния между частицами много больше длины волны излучения  , что приводит к неравенству n<<1/ , что приводит к неравенству n<<1/ 3. Используя значения реальных счетных концентраций молекул воздуха и аэрозольных частиц в атмосфере Земли, легко проверить, что условие n << 1/d3 всегда выполняется, в вот условие n<<1/ 3. Используя значения реальных счетных концентраций молекул воздуха и аэрозольных частиц в атмосфере Земли, легко проверить, что условие n << 1/d3 всегда выполняется, в вот условие n<<1/ 3, справедливое в коротковолновой области спектра для аэрозольных частиц, для молекул атмосферных газов оказывается нарушенным. Однако считается, что, поскольку реально свет рассеивается не на молекулах, а на флуктуациях плотности воздуха (т.е. воздух рассматривается уже как сплошная среда) этим нарушением можно пренебречь . При расчете поля радиации элементарный объем среды выбирается таким образом, чтобы в нем происходил один акт рассеяния. Такой объем различен для частиц разного размера (для капель облака он составляет около 10-20 мкм, для молекул атмосферных газов (флуктуаций) – 0,5.10-3мкм. Таким образом, рассеивающая свет среда оказывается не непрерывной. С другой стороны, необходимо отметить, что нарушение даже обоих условий может происходить в случае наличия в воздухе крупных частиц (например, облачных капель). Действительно, учитывая большие размеры капли (десятки и сотни мкм), вблизи ее находится значительное количество молекул атмосферных газов, для которых нарушены оба условия. Поэтому для таких случаев вопрос о точности применимости “правил сложения” нуждается в дальнейшем исследовании. 3, справедливое в коротковолновой области спектра для аэрозольных частиц, для молекул атмосферных газов оказывается нарушенным. Однако считается, что, поскольку реально свет рассеивается не на молекулах, а на флуктуациях плотности воздуха (т.е. воздух рассматривается уже как сплошная среда) этим нарушением можно пренебречь . При расчете поля радиации элементарный объем среды выбирается таким образом, чтобы в нем происходил один акт рассеяния. Такой объем различен для частиц разного размера (для капель облака он составляет около 10-20 мкм, для молекул атмосферных газов (флуктуаций) – 0,5.10-3мкм. Таким образом, рассеивающая свет среда оказывается не непрерывной. С другой стороны, необходимо отметить, что нарушение даже обоих условий может происходить в случае наличия в воздухе крупных частиц (например, облачных капель). Действительно, учитывая большие размеры капли (десятки и сотни мкм), вблизи ее находится значительное количество молекул атмосферных газов, для которых нарушены оба условия. Поэтому для таких случаев вопрос о точности применимости “правил сложения” нуждается в дальнейшем исследовании.
Объемные коэффициенты взаимодействия излучения с атмосферой выражаются согласно соотношениям (1.2.11) через сечения рассеяния и поглощения, следовательно, важнейшей задачей является теоретический расчет этих сечений. Методы таких расчетов основаны на описании физических процессов взаимодействия излучения с веществом . Но поскольку мы договорились их не рассматривать, приведем соответствующие формулы уже в готовом “инженерном” виде, отсылая читателя за подробностями к указанной ниже литературе.
Объемный коэффициент и индикатриса молекулярного рассеяния равны ,
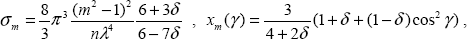 |
(1.2.14) |
где m – показатель преломления воздуха, n – счетная концентрация молекул воздуха,  – длина волны света, – длина волны света, 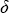 – фактор деполяризации, для воздуха – фактор деполяризации, для воздуха 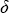 = 0,035. Вывод соотношений (1.2.14) приведен, например, в монографиях , (традиционная для оптики атмосферы молекулярная теория рассеяния) и в учебнике (теория рассеяния на флуктуациях плотности воздуха). Из известного термодинамического соотношения получаем счетную концентрацию , = 0,035. Вывод соотношений (1.2.14) приведен, например, в монографиях , (традиционная для оптики атмосферы молекулярная теория рассеяния) и в учебнике (теория рассеяния на флуктуациях плотности воздуха). Из известного термодинамического соотношения получаем счетную концентрацию ,
где P – давление воздуха, T – температура воздуха, k – постоянная Больцмана. Для зависимости показателя преломления воздуха от длины волны, давления, температуры и влажности используем полуэмпирическое соотношение из монографии
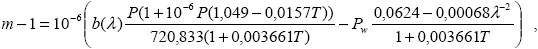
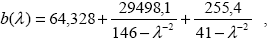 |
(1.2.16) |
где Pw – парциальное давление водяного пара. В формулах (1.2.16) длина волны измеряется в мкм, давление – в мм.рт.ст., температура – в градусах Цельсия.
В рассматриваемом коротковолновом спектральном диапазоне имеющиеся исходные данные для расчета сечений молекулярного поглощения представлены в двух разновидностях.
Данные первого типа приведены в виде таблиц зависимости экспериментально измеренных сечений от длины волны и в некоторых случаях от температуры, т.е. Ca,i( ,T). К сожалению, в настоящее время в свободном доступе практически отсутствуют подробные базы данных по указанным сечениям, поэтому в конкретных расчетах мы использовали банк таких данных, собранный в основном по сведениям, приведенным в работах [10,11] а также значения, взятые, с разрешения авторов В.В. Розанова и Ю.М.Тимофеева из базы данных компьютерного кода GOMETRAN [12,13]. Сечение молекулярного поглощения конкретного газа (индекс i опускаем) для данных первого типа вычисляется элементарной линейной интерполяцией по таблице: ,T). К сожалению, в настоящее время в свободном доступе практически отсутствуют подробные базы данных по указанным сечениям, поэтому в конкретных расчетах мы использовали банк таких данных, собранный в основном по сведениям, приведенным в работах [10,11] а также значения, взятые, с разрешения авторов В.В. Розанова и Ю.М.Тимофеева из базы данных компьютерного кода GOMETRAN [12,13]. Сечение молекулярного поглощения конкретного газа (индекс i опускаем) для данных первого типа вычисляется элементарной линейной интерполяцией по таблице:
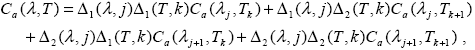 |
(1.2.17) |
где
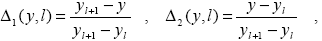
и номера j и k выбираются по точкам сетки таблицы из условий  j j 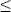 l l 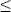  j+1, Tk j+1, Tk 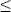 T T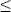 Tk+1. Если температурная зависимость отсутствует, то в (1.2.17) достаточно формально положить Tk+1. Если температурная зависимость отсутствует, то в (1.2.17) достаточно формально положить 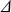 1(T,k)=1, 1(T,k)=1, 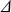 2(T,k)=0. 2(T,k)=0.
Данные второго типа представляют собой описания отдельных линий поглощения газов (параметры тонкой структуры). Теоретические аспекты расчетов с помощью этих данных подробно описаны, например, в монографии [14]. Для конкретных расчетов мы использовали базу данных HITRAN-92 [15]. Объемный коэффициент молекулярного поглощения по данным второго типа, зависящий от температуры T и давления воздуха P, вычисляется как
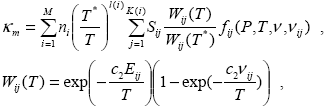 |
(1.2.18) |
где суммирование по индексу i ведется по всем газам, суммирование по j ‑ по всем линиям поглощения данного газа, T* ‑ температура, для которой приведена спектроскопическая информация (T*=296К),  (i)=1 для линейных молекул и (i)=1 для линейных молекул и  (i)=1,5 для прочих, fij ‑ функция контура спект-ральной линии, n ‑ волновое число, соответствующее длине волны (i)=1,5 для прочих, fij ‑ функция контура спект-ральной линии, n ‑ волновое число, соответствующее длине волны  ( ( = 1/ = 1/ ), c2 ‑ вторая радиационная постоянная, Sij, Eij, ), c2 ‑ вторая радиационная постоянная, Sij, Eij,  ij ‑ параметры линии из базы данных HITRAN-92: интенсивность, энергия перехода в единицах волнового числа и волновое число центра линии соответственно. Для функции контура спектральной линии fij в общем случае не существует явного аналитического выражения. Поэтому в конкретных расчетах применялась аппроксимация, предложенная в работе [16]: ij ‑ параметры линии из базы данных HITRAN-92: интенсивность, энергия перехода в единицах волнового числа и волновое число центра линии соответственно. Для функции контура спектральной линии fij в общем случае не существует явного аналитического выражения. Поэтому в конкретных расчетах применялась аппроксимация, предложенная в работе [16]:
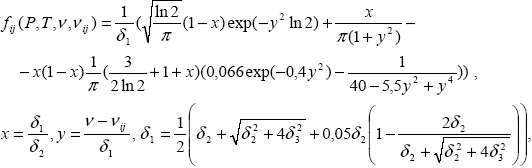
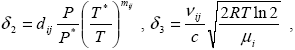 |
(1.2.19) |
где P* ‑ давление, для которого приведена спектроскопическая информация (P*=1013 мбар), c - скорость света в вакууме, R ‑ универсальная газовая постоянная, 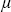 i ‑ молекулярная масса газа, dij, i ‑ молекулярная масса газа, dij, 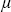 i ‑ параметры линии базы HITRAN-92: полуширина линии поглощения вызванная столкновениями с молекулами воздуха и коэффициент температурной зависимости соответственно.5 i ‑ параметры линии базы HITRAN-92: полуширина линии поглощения вызванная столкновениями с молекулами воздуха и коэффициент температурной зависимости соответственно.5
Расчет сечений аэрозольного рассеяния и поглощения, а также аэрозольной индикатрисы рассеяния выполняется на основе модельных представлений. Аэрозольные частицы аппроксимируют фигурами определенной геометрической формы, размера и известного химического состава. Обычно рассматривают однородные сферические частицы. Расчет оптических характеристик для таких частиц выполняется по формулам теории Ми, которые мы приводить не будем, отсылая читателя к соответствующей литературе: основы теории и вывод формул в монографиях [17,18], переход к характеристикам элементарного объема в монографии [19], практические алгоритмы расчетов в работах [18,20,21]. Важным процессом, влияющим на оптические характеристики аэрозольных частиц, особенно в тропосфере, является их обводнение – адсорбция на поверхности частиц молекул воды. Это приводит к существенным изменением оптических свойств аэрозолей в зависимости от влажности воздуха. Моделью обводненной частицы служит двухслойная частица – “шар в оболочке”, для которой методы расчета оптических характеристик можно найти в работах [18,22,23]. В силу громоздкости расчетов оптических характеристик аэрозольных частиц их практически всегда проводят заранее, используя в задачах переноса излучения уже известные аэрозольные объемные коэффициенты поглощения, рассеяния и индикатрисы, приведенные в виде таблиц. Такие данные, а также исходные данные для выполнения указанных расчетов являются основой аэрозольных моделей. В настоящее время аэрозольным моделям посвящена весьма обширная литература, обзор которой не входит в круг обсуждаемых вопросов. Укажем только, что выбор или создание аэрозольной модели определяется, прежде всего, условиями конкретной задачи. Именно так мы и поступим, приведя ссылки на соответствующие модели в гл. 5.
Индикатриса аэрозольного рассеяния получается в обсуждавшихся выше расчетах как дискретная таблица с сеткой по углам рассеяния. В ряде задач это неудобно и требуется аппроксимировать ее непрерывной функцией. Одной из наиболее широко используемых аппроксимаций является функция Хэньи‑Гринстейна [24] ,
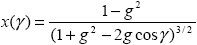 |
(1.2.20) |
где  – параметр аппроксимации (0 – параметр аппроксимации (0 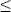  < 1). Эта функция описывает основное свойство аэрозольных индикатрис – вытянутость вперед (преобладание рассеяния в переднюю полусферу 0 < 1). Эта функция описывает основное свойство аэрозольных индикатрис – вытянутость вперед (преобладание рассеяния в переднюю полусферу 0 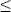  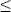 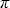 /2 над рассеянием в заднюю полусферу /2 над рассеянием в заднюю полусферу 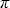 /2 /2 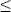  £ £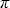 ) и, как мы выясним позже, является очень удобной для теоретических расчетов. Однако она описывает реальные аэрозольные индикатрисы рассеяния с большой погрешностью (нередко с очень большой) [25]. Поэтому пользоваться этой функцией можно только при условии оценки погрешности, вносимой ею в расчеты. Более подробно мы обсудим вопросы аппроксимации аэрозольной индикатрисы в гл. 5. ) и, как мы выясним позже, является очень удобной для теоретических расчетов. Однако она описывает реальные аэрозольные индикатрисы рассеяния с большой погрешностью (нередко с очень большой) [25]. Поэтому пользоваться этой функцией можно только при условии оценки погрешности, вносимой ею в расчеты. Более подробно мы обсудим вопросы аппроксимации аэрозольной индикатрисы в гл. 5.
1 В другой терминологии, сечение направленного рассеяния именуют “дифференциальным сечением рассеяния”, а сечение рассеяния ‑ “интегральным сечением рассеяния”. Смысл этих названий очевиден из соотношений (1.2.1) - (1.2.4).
2Заметим, что индикатриса определяет рассеяние лишь в случае неполяризованного исходного света. После рассеяния (как молекулярного, так и аэрозольного) свет становится уже поляризованным и его последующие (второе и т.д.) рассеяния уже не могут быть описаны с привлечением только понятия индикатрисы. Таким образом, теория рассеяния, не учитывающая поляризацию, является приближенной. В общем случае оценки точности такого приближения [6] дают погрешность менее 5%. Для конкретных вычислительных задач, в принципе, необходимо проводить собственные оценки, о чем будет идти речь в следующих разделах.
3Заметим, что введенные объемные коэффициенты имеют размерность обратной длины, а такие величины принято называть “линейными”, а не “объемными”. Чуть ниже мы обоснуем это терминологическое противоречие.
4Именно поэтому для коэффициента употребляется термин “объемный”, а не “линейный”. Он определяется счетной концентрацией, т.е. числом частиц в единице объема воздуха.
5Заметим, что спектроскопические данные, как первого, так и второго типов получены из экспериментальных измерений, следовательно, содержат погрешности. Кроме того, помимо аппроксимации, формулы контура линии (1.2.19) и сама “теоретическая” формула (1.2.18) являются некоторым приближением. Поэтому расчет по (1.2.18), (1.2.19) связан с определенной погрешностью. Но реально молекулярное поглощение в коротковолновой области спектра достаточно слабое, поэтому договоримся эти погрешности не учитывать. |