По современным представлениям свет (излучение, радиация) является электромагнитными волнами, проявляющими в том числе и квантовые свойства, поэтому, строго говоря, процессы его распространения в атмосфере следует описывать в рамках электродинамики и квантовой механики. Однако для многих задач, включая и решаемые в данной книге, целесообразно абстрагироваться от электромагнитной природы излучения и рассматривать его лишь как поток энергии. Определяемые через энергию характеристики излучения называются радиационными. Для оптики такое рассмотрение является достаточно стандартным, поскольку частоты электромагнитных волн в оптическом диапазоне очень велики и измерению реально доступна лишь энергия волны, принятая приемником за весьма большое число ее периодов, а не мгновенные значения напряженности электрического поля. С электромагнитной природой солнечного излучения, а именно с тем свойством, что электромагнитные волны являются поперечными связано также явление поляризации, проявляющееся в зависимости процессов взаимодействия излучения с веществом (преломления, рассеяния, отражения) от конкретной геометрии колебаний вектора электрического поля в плоскости, перпендикулярной распространению волны. Ниже мы будем пользоваться приближением неполяризованного излучения, т.е. считать, что указанная выше зависимость не имеет места. Оценка точности этого приближения будет приведена позднее с учетом конкретных рассматриваемых задач.
В излучении, проходящем через атмосферу Земли, выделяют следующие основные типы излучений (и их энергий): прямое солнечное, т.е. излучение, пришедшее в данную точку непосредственно от Солнца; рассеянное солнечное, т.е. излучение Солнца, испытавшее рассеяние в атмосфере; отраженное от подстилающей поверхности солнечное излучение; собственное излучение атмосферы (тепловое излучение) и собственное излучение поверхности (тепловое). Совокупность данных излучений создает в атмосфере Земли поле излучения, которое характеризуется наличием энергии излучения различных спектральных диапазонов и приходящей с различных направлений. Как видно из приведенного выше перечисления, все излучение в атмосфере Земли по происхождению можно разделить на солнечное и собственное (тепловое). В этой книге мы ограничимся рассмотрением лишь солнечного излучения в области спектра 0,3-1,0 мкм, где энергией собственного излучения атмосферы и поверхности по сравнению с энергией солнечного излучения можно пренебречь. В дальнейшем, для определенности, указанную область будем именовать коротковолновой областью спектра. Заметим, впрочем, что приводимые ниже определения радиационных характеристик не связаны с этим ограничением и справедливы и для инфракрасной, и для микроволновой областей спектра.
В оптике для теоретического описания различных процессов широко используется понятие монохроматических параллельных пучков лучей, (плоских электромагнитных волн, имеющих строго одно направление и конкретную длину волны) . Именно в таком виде стандартно задается солнечное излучение при описании его взаимодействия с различными объектами. При этом постулируется принцип независимости подобных монохроматических пучков при их наложении, т.е. взаимодействие с объектом излучения, приходящего одновременно с разных направлений, рассматривается как сумма независимых взаимодействий по каждому из направлений. Физической основой принципа независимости является некогерентность естественных источников излучения 1 .
Для поля излучения в атмосфере естественно воспользоваться этим стандартным приемом, т.е. свести его к сумме невзаимодействующих параллельных монохроматических пучков лучей. При этом интересующую нас энергию излучения нельзя непосредственно переносить на отдельный пучок, поскольку, если энергия конечна для некоторого интервала длин волн и направлений, то для одной длины волны и одного направления она станет бесконечно малой величиной. Очевидно, что для характеристики излучения следует перейти от энергии к ее распределению по спектру и направлениям.
Рассмотрим некоторый излучающий объект (рис.1.1.), причем в качестве такового будем подразумевать не обязательно собственно источник излучения, но и отражающий или рассеивающий внешнее излучение объект. Выберем на поверхности объекта элементарную площадку dS, опишем вокруг нормали к ней 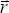 телесный угол d телесный угол d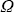 . Тогда энергия излучения пропорциональна площади dS, телесному углу d . Тогда энергия излучения пропорциональна площади dS, телесному углу d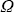 , а также рассматриваемым интервалам длин волн [ , а также рассматриваемым интервалам длин волн [ , ,  +d +d ] и времени [t, t + dt]. Интенсивностью излучения (по [2, 3]) на длине волны ] и времени [t, t + dt]. Интенсивностью излучения (по [2, 3]) на длине волны  в направлении в момент времени t называется коэффициент пропорциональности энергии излучения dE величинам dS, d в направлении в момент времени t называется коэффициент пропорциональности энергии излучения dE величинам dS, d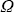 , d , d и dt, т.е. и dt, т.е.
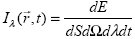 . . |
(1.1.1) |
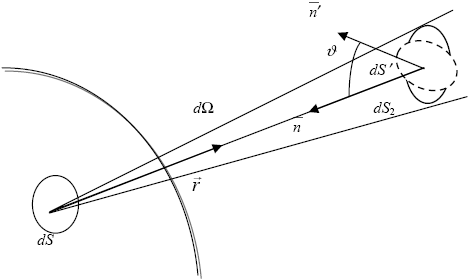
Рисунок 1.1. К определению интенсивности и потока излучения.
Во многих случаях нас интересует не излучаемая объектом энергия, а энергия поля излучения, приходящая на объект (например, на вход измерительного прибора). Тогда легко трансформировать данное выше определение интенсивности. Рассмотрим излучающий объект и поместим вторую, такую же по площади элементарную площадку dS2 = dS на некотором (любом) расстоянии от него (рис.1.1.) Пусть излучающий объект находится в вакууме, т.е. излучение по пути от объекта до dS2 не испытывает никаких взаимодействий. Пусть площадка dS2 перпендикулярна направлению 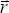 , тогда телесный угол, под которым в направлении , тогда телесный угол, под которым в направлении 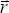 видна dS2 с площадки dS, очевидно, равен телесному углу, под которым в противоположном направлении (- видна dS2 с площадки dS, очевидно, равен телесному углу, под которым в противоположном направлении (-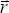 ) видна dS с площадки dS2. Но тогда равны и энергии dE, приходящие на dS и dS2 и мы получаем следствие из приведенного выше определения интенсивности: интенсивностью излучения I ) видна dS с площадки dS2. Но тогда равны и энергии dE, приходящие на dS и dS2 и мы получаем следствие из приведенного выше определения интенсивности: интенсивностью излучения I ( (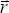 ,t), приходящего из направления ,t), приходящего из направления 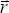 на элементарную площадку dS, перпендикулярную на элементарную площадку dS, перпендикулярную 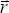 , на длине волны , на длине волны  в момент времени t называется коэффициент пропорциональности энергии излучения dE величинам dS, d в момент времени t называется коэффициент пропорциональности энергии излучения dE величинам dS, d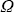 , d , d и dt, т.е. (1.1.1). Подчеркнем важное требование перпендикулярности площадки dS направлению как в определении интенсивности уходящего излучения ( и dt, т.е. (1.1.1). Подчеркнем важное требование перпендикулярности площадки dS направлению как в определении интенсивности уходящего излучения (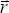 - вектор нормали к поверхности), так и приходящего. - вектор нормали к поверхности), так и приходящего.
Приведенное определение интенсивности как некоего “коэффициента пропорциональности” носит несколько формальный характер. Поэтому часто дают такое “физическое” определение: интенсивностью излу-чения называется энергия, приходящая в единицу времени из единицы телесного угла в единичном интервале длин волн на единицу площади поверхности, перпендикулярной направлению приходящего излучения. Это определение вполне корректно, если уточнить, что имеется в виду энергия, соответствующая не реальным единичным масштабам (сек, стер, мкм, см2), а дифференциальным dt, d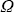 , d , d , dS, и которая затем приводится к единичным масштабам, что и отражает формула (1.1.1). , dS, и которая затем приводится к единичным масштабам, что и отражает формула (1.1.1).
Пусть теперь площадка dS', на которую падает излучение, не перпендикулярна его направлению, а образует с ним угол  (рис.1.1.) Обозначим угол падения излучения на площадку ‑ угол между направ-лением, обратным направлению распространения излучения и нормалью к площадке как (рис.1.1.) Обозначим угол падения излучения на площадку ‑ угол между направ-лением, обратным направлению распространения излучения и нормалью к площадке как 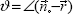 . В этом случае в определении интенсивности как коэффициента пропорциональности (1.1.1) мы должны в качестве площади dS использовать проекцию площадки dS' на плоскость, перпендикулярную направлению распространения излучения. Но эта проекция равна dS=dS'cos . В этом случае в определении интенсивности как коэффициента пропорциональности (1.1.1) мы должны в качестве площади dS использовать проекцию площадки dS' на плоскость, перпендикулярную направлению распространения излучения. Но эта проекция равна dS=dS'cos . Тогда из формулы (1.1.1) для энергии dE, приходящей на наклонно ориентированную площадку dS ' получаем . . Тогда из формулы (1.1.1) для энергии dE, приходящей на наклонно ориентированную площадку dS ' получаем .
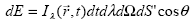 |
(1.1.2) |
Определенной таким образом энергии удобно приписать знак. Действительно, если мы фиксируем конкретную сторону поверхности dS' и понимаем под нормалью нормаль именно к этой стороне, то угол  будет меняться от 0 до будет меняться от 0 до 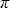 , а его косинус – от +1 до -1. Таким образом, энергия, приходящая на площадку, будет положительной, а уходящая с нее – отрицательной. Что имеет ясный физический смысл положительного источника и отрицательного стока энергии для dS'. Определим теперь (согласно [2,3]) поток излучения F , а его косинус – от +1 до -1. Таким образом, энергия, приходящая на площадку, будет положительной, а уходящая с нее – отрицательной. Что имеет ясный физический смысл положительного источника и отрицательного стока энергии для dS'. Определим теперь (согласно [2,3]) поток излучения F (t) (часто уточняют – полный спектральный поток) как коэффициент пропорциональности энергии излучения dE', приходящей в интервалах длин волн [ (t) (часто уточняют – полный спектральный поток) как коэффициент пропорциональности энергии излучения dE', приходящей в интервалах длин волн [ , , + d + d ] и времени [t, t + dt] на площадку dS' со всех направлений, значениям dt, d ] и времени [t, t + dt] на площадку dS' со всех направлений, значениям dt, d , dS', т.е. , dS', т.е.
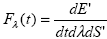 . . |
(1.1.3) |
Приведем “физическое” определение потока, которое часто употребляют вместо “формального” (1.1.3). Потоком излучения называется энергия, приходящая на единичную площадку, в единицу времени в единичном интервале длин волн. Это определение корректно согласуется с выражением (1.1.3), если только под энергией понимать разность приходящей и уходящей энергии и использовать дифференциальные масштабы площади, времени и длины волны. Исходя из такой трактовки, в дальнейшем будем, как синонимом потока, пользоваться термином энергия, подразумевая величину энергии, приходящейся на единицу площади, времени и длины волны.
Введем для характеристики направления приходящего на dS' излучения помимо угла  еще и азимут еще и азимут 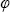 , отсчитываемый как угол между проекцией вектора на плоскость dS' и (произвольно) выбранным направлением на этой плоскости (0 , отсчитываемый как угол между проекцией вектора на плоскость dS' и (произвольно) выбранным направлением на этой плоскости (0 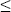 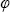 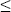 2 2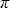 ). То есть, фактически, договоримся для направлений использовать сферическую систему координат. Энергия dE', приходящая на площадку dS' со всех направлений, выражается через энергию из конкретного направления dE( ). То есть, фактически, договоримся для направлений использовать сферическую систему координат. Энергия dE', приходящая на площадку dS' со всех направлений, выражается через энергию из конкретного направления dE( , ,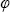 ) как ) как
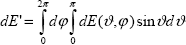 , ,
где интегрирование ведется по всей сфере, или, учитывая известное выражение для элемента телесного угла в сферических координатах d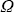 = d = d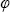 sin sin d d , как , как
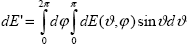 . .
Подставляя это выражение в (1.1.3) с учетом (1.1.2) получаем формулу, выражающую поток через интенсивность излучения .
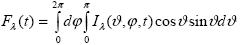 |
(1.1.4) |
Интенсивность излучения в атмосфере помимо направления ( , ,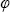 ), длины волны ), длины волны  и времени t зависит еще и от точки нахождения площадки dS. Вследствие сферичности Земли и ее атмосферы, положение этой точки наиболее удобно задавать в сферической системе координат с началом в центре Земли. Однако, учитывая то обстоятельство, что толщина атмосферы много меньше радиуса Земли, в очень многих задачах атмосферу можно считать плоской, конкретно – ограниченной двумя (бесконечными) плоскостями: нижней границей – подстилающей поверхностью и верхней границей – уровнем, выше которого взаимодействием излучения с атмосферой можно пренебречь. Договоримся в дальнейшем рассматривать только это приближение плоскопараллельной атмосферы. Обоснование целесообразности его использования для решения конкретных задач будет дано в разделе 1.3. Тогда положение площадки dS' можно характеризовать декартовыми координатами (x,y,z), причем в качестве z естественно выбрать высоту (т.е. направить ось Z перпендикулярно плоскостям границ атмосферы в направлении от нижней к верхней). Итак, в общем случае интенсивность излучения в атмосфере можно записать как I и времени t зависит еще и от точки нахождения площадки dS. Вследствие сферичности Земли и ее атмосферы, положение этой точки наиболее удобно задавать в сферической системе координат с началом в центре Земли. Однако, учитывая то обстоятельство, что толщина атмосферы много меньше радиуса Земли, в очень многих задачах атмосферу можно считать плоской, конкретно – ограниченной двумя (бесконечными) плоскостями: нижней границей – подстилающей поверхностью и верхней границей – уровнем, выше которого взаимодействием излучения с атмосферой можно пренебречь. Договоримся в дальнейшем рассматривать только это приближение плоскопараллельной атмосферы. Обоснование целесообразности его использования для решения конкретных задач будет дано в разделе 1.3. Тогда положение площадки dS' можно характеризовать декартовыми координатами (x,y,z), причем в качестве z естественно выбрать высоту (т.е. направить ось Z перпендикулярно плоскостям границ атмосферы в направлении от нижней к верхней). Итак, в общем случае интенсивность излучения в атмосфере можно записать как I (x,y,z, (x,y,z, , ,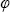 ,t). Для естественных источников излучения (в частности – солнечного) изменением интенсивности излучения со временем можно пренебречь по сравнению с рассматриваемыми в конкретных задачах временными масштабами (например, по сравнению со скоростью регистрации интенсивности излучения прибором). Такое поле излучения называется стационарным. Далее, можно пренебречь влиянием на поле излучения горизонтальных неоднородностей атмосферы по сравнению с вертикальными, т.е. не рассматривать зависимость интенсивности излучения от координат x и y. Такое поле излучения называется горизонтально-однородным. Договоримся в дальнейшем рассматривать только стационарные, горизонтально-однородные поля излучения. Кроме того, следуя традициям , , договоримся опускать у монохроматических величин индекс ,t). Для естественных источников излучения (в частности – солнечного) изменением интенсивности излучения со временем можно пренебречь по сравнению с рассматриваемыми в конкретных задачах временными масштабами (например, по сравнению со скоростью регистрации интенсивности излучения прибором). Такое поле излучения называется стационарным. Далее, можно пренебречь влиянием на поле излучения горизонтальных неоднородностей атмосферы по сравнению с вертикальными, т.е. не рассматривать зависимость интенсивности излучения от координат x и y. Такое поле излучения называется горизонтально-однородным. Договоримся в дальнейшем рассматривать только стационарные, горизонтально-однородные поля излучения. Кроме того, следуя традициям , , договоримся опускать у монохроматических величин индекс  , если только речь не идет о явной зависимости от длины волны. С учетом перечисленных допущений формула связи потока и интенсивности излучения (1.1.4) запишется как . , если только речь не идет о явной зависимости от длины волны. С учетом перечисленных допущений формула связи потока и интенсивности излучения (1.1.4) запишется как .
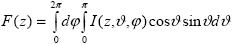 . . |
(1.1.5) |
Поскольку в атмосфере мы выделили конкретное направление – ось Z (высоты), то от него естественно отсчитывать и угол  . Такой угол называется зенитным углом приходящего излучения (он характеризует отклонение его от зенита). Угол . Такой угол называется зенитным углом приходящего излучения (он характеризует отклонение его от зенита). Угол  равен нулю, если излучение идет из зенита, и равен нулю, если излучение идет из зенита, и 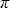 , если из надира. Азимут по-прежнему будем отсчитывать от произвольного направления в плоскости, параллельной границам атмосферы. Тогда интеграл (1.1.5) можно записать как сумму двух – по верхней и нижней полусферам: , если из надира. Азимут по-прежнему будем отсчитывать от произвольного направления в плоскости, параллельной границам атмосферы. Тогда интеграл (1.1.5) можно записать как сумму двух – по верхней и нижней полусферам:
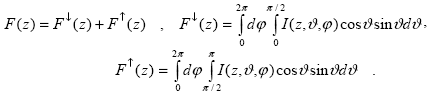 |
(1.1.6) |
Величина F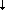 (z) называется нисходящим потоком, величина F (z) называется нисходящим потоком, величина F (z) – восходящим потоком, оба эти потока также называются полусферическими. Физический смысл этих определений очевиден. Нисходящий поток – это энергия излучения, проходящая через уровень высоты z вниз, т.е. к поверхности Земли, а восходящий поток – энергия, проходящая вверх – от подстилающей поверхности. Нисходящий поток всегда положителен (cos (z) – восходящим потоком, оба эти потока также называются полусферическими. Физический смысл этих определений очевиден. Нисходящий поток – это энергия излучения, проходящая через уровень высоты z вниз, т.е. к поверхности Земли, а восходящий поток – энергия, проходящая вверх – от подстилающей поверхности. Нисходящий поток всегда положителен (cos > 0), восходящий – всегда отрицателен (cos > 0), восходящий – всегда отрицателен (cos < 0). В практических приложениях (например, при измерениях) принято рассматривать оба этих потока как положительные. Договоримся следовать этой традиции. Тогда для восходящего потока cos < 0). В практических приложениях (например, при измерениях) принято рассматривать оба этих потока как положительные. Договоримся следовать этой традиции. Тогда для восходящего потока cos в выражении (1.1.6) следует брать по модулю, а (полный) поток запишется как разность полусферических потоков F(z)=F в выражении (1.1.6) следует брать по модулю, а (полный) поток запишется как разность полусферических потоков F(z)=F (z) - F (z) - F (z), определенную таким образом величину часто называют (спектральным) радиационным балансом. (z), определенную таким образом величину часто называют (спектральным) радиационным балансом.
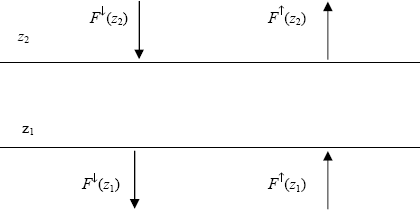
Рисунок 1.2. К определению притока излучения
Рассмотрим два уровня в атмосфере, определяемые высотами z1 и z2 (рис.1.2.) Найдем энергию солнечного излучения B(z1,z2) (на единицу площади, времени и длины волны), поглощенного атмосферой между этими уровнями. Очевидно, для этого следует из входящей в слой энергии вычесть выходящую энергию, т.е. .
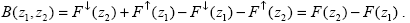 |
(1.1.7) |
Величина B(z1,z2) называется притоком излучения или лучистым притоком в слое от высоты z1 до высоты z2. Она имеет важнейшее значение в изучении энергетики атмосферы, так как, очевидно, определяет ее нагрев, и при исследовании состава атмосферы, поскольку по характеру спектральной зависимости B(z1,z2) можно судить о типе и содержании конкретных поглощающих субстанций (атмосферных газов и аэрозолей) в рассматриваемом слое. Соответственно важнейшее значение для указанного класса задач имеют и величины полусферических потоков излучения, определяющие величину лучистого притока.
Для обеспечения возможности сравнения величин лучистых притоков в атмосферных слоях различной толщины, значение B(z1,z2) нормируют на толщину слоя
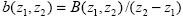 . . |
(1.1.8) |
Заметим, что определение нормированного притока (1.1.8) с учетом (1.1.7) дает возможность в теории рассматривать его как непрерывную функцию высоты, записав через производную баланса (полного потока) 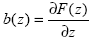 . .
Выше, давая определения интенсивности и потока излучения, мы рассматривали поле излучения, т.е. ситуацию, когда излучение распространяется по различным направлениям. В сущности, этим можно бы и ограничиться, поскольку строго параллельных (однонаправленных) пучков лучей не может существовать в силу волновых свойств света . Однако часто излучение некоторых объектов можно аппроксимировать как однонаправленное без потери точности. В интересующих нас задачах таким однонаправленным излучением практически всегда считается приходящее на верхнюю границу атмосферы излучение Солнца. Действительно, из-за малости радиусов Земли и Солнца по сравнению с расстоянием между ними, угловым расхождением пучка солнечных лучей, приходящих на Землю, можно пренебречь. Таким образом, мы будем рассматривать случай плоскопараллельной горизонтально-однородной атмосферы освещаемой сверху параллельными солнечными лучами. Поскольку таким лучам, имеющим только одно направление, мы должны приписать определенную энергию, возникают некоторые трудности при применении приведенных выше определений к данному случаю.
Определение интенсивности излучения в соответствии с формулой (1.1.1) неприменимо, поскольку в нем отсутствует зависимость энергии dE от телесного угла d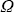 (следуя формально соотношению (1.1.1) получим нулевую интенсивность). Определение же потока (1.1.3) применимо. Поэтому для строго параллельных (однонаправленных) лучей имеет смысл говорить именно о потоке излучения. При этом для различно ориентированных площадок dS' очевидно будет наблюдаться зависимость энергии dE' в (1.1.3) от площади проекции площадки dS' на направление распространения излучения, что дает (следуя формально соотношению (1.1.1) получим нулевую интенсивность). Определение же потока (1.1.3) применимо. Поэтому для строго параллельных (однонаправленных) лучей имеет смысл говорить именно о потоке излучения. При этом для различно ориентированных площадок dS' очевидно будет наблюдаться зависимость энергии dE' в (1.1.3) от площади проекции площадки dS' на направление распространения излучения, что дает
F( )=F0cos )=F0cos , , |
(1.1.9) |
где F0 ‑ поток излучения для перпендикулярно падающих лучей, F( ) - поток для угла падения ) - поток для угла падения  . .
Для оптики и энергетики земной атмосферы фундаментальное значение имеет поток F0 солнечного излучения, падающего на верхнюю границу атмосферы. Этот поток – энергия излучения, приходящая на перпендикулярную лучам площадку единичной площади на верхней границе атмосферы в единицу времени в единичном интервале длин волн для среднего расстояния от Земли до Солнца ‑ называется спектральной солнечной постоянной. График ее зависимости от длины волны по данным работы приведен на рис.1.3. Что касается интенсивности излучения для этого случая, то ее формально можно определить, исходя из выражения (1.1.5). Действительно, чтобы выполнялись соотношения (1.1.5) и (1.1.9) необходимо положить
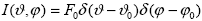 |
(1.1.10) |
где 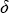 () – дельта-функция [5], ( () – дельта-функция [5], ( 0, 0,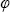 0) ‑ направление параллельного пучка лучей (зенитный угол и азимут Солнца в нашем случае). Напомним, что дельта-функция определена как 0) ‑ направление параллельного пучка лучей (зенитный угол и азимут Солнца в нашем случае). Напомним, что дельта-функция определена как
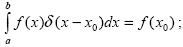
никакая “настоящая” функция не обладает таким свойством, поэтому дельта-функция есть символическая запись, грубо говоря, она не существует вне интегралов.
Исходя из формулы (1.1.10) можно для случая параллельного пучка лучей говорить о численном равенстве потока, приходящего на перпендикулярную лучам площадку, и интенсивности излучения, однако, следует учитывать, что это равенство чисто формальное, хотя бы потому, что поток и интенсивность имеют разные размерности (вот в (1.1.10) с размерностями все в порядке).
В заключение рассмотрим теоретические аспекты процессов измерения интенсивностей и потоков. Реально на измерительный элемент прибора воздействует энергия излучения, которую согласно выражению (1.1.1) в общем случае следует записать
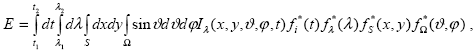
где I (x,y, (x,y, , ,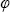 ,t) ‑ интенсивность излучения, приходящая в точку входного элемента (входной щели) прибора с координатами (x,y); [t1, t2] ‑ интервал времени регистрации входного сигнала; [ ,t) ‑ интенсивность излучения, приходящая в точку входного элемента (входной щели) прибора с координатами (x,y); [t1, t2] ‑ интервал времени регистрации входного сигнала; [ 1, 1,  2] ‑ диапазон длин волн регистрации; ft*(t), f 2] ‑ диапазон длин волн регистрации; ft*(t), f *( *( ), fS*(x,y), f ), fS*(x,y), f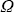 *( *( , ,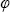 ) ‑ аппаратные функции прибора, характеризующие трансформацию им сигнала в зависимости от времени t, длины волны ) ‑ аппаратные функции прибора, характеризующие трансформацию им сигнала в зависимости от времени t, длины волны  , точки на входном элементе (x, y) и направления падающего излучения ( , точки на входном элементе (x, y) и направления падающего излучения ( , ,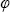 ) соответственно. Интегрирование по площади S выполняется по поверхности входного элемента, по телесному углу ) соответственно. Интегрирование по площади S выполняется по поверхности входного элемента, по телесному углу 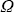 – по углу зрения прибора. Приборы калибруются так, чтобы выдавать непосредственно измеряемую величину интенсивности, с теоретической точки зрения это означает нормировку аппаратных функций – по углу зрения прибора. Приборы калибруются так, чтобы выдавать непосредственно измеряемую величину интенсивности, с теоретической точки зрения это означает нормировку аппаратных функций
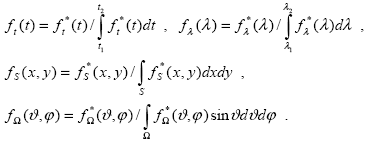
Тогда измеряемая интенсивность I выражается через реальную интенсивность I (x,y, (x,y, , ,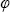 ,t) следующим соотношением: ,t) следующим соотношением:
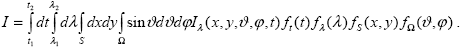 . . |
(1.1.11) |
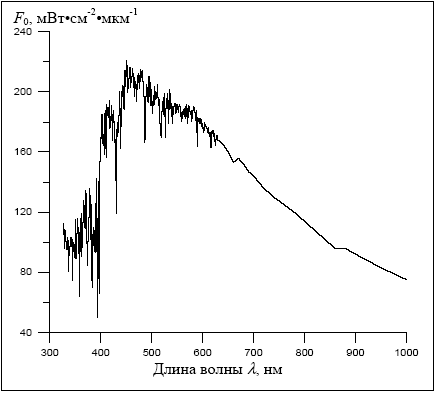
Рисунок 1.3. Спектральная солнечная постоянная по данным работы [4]
Действительно, для нормированных аппаратных функций, если I (x,y, (x,y, , ,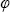 ,t) = I0 = const, то по (1.1.11) и I =I0. ,t) = I0 = const, то по (1.1.11) и I =I0.
При измерениях интенсивности излучения угол зрения прибора делают предельно малым, в этом случае можно пренебречь всеми зависимостями, кроме длины волны. Тогда основной характеристикой прибора является спектральная аппаратная функция f ( ( ), которую в дальнейшем будем именовать просто аппаратной функцией. Если интенсивность излучения в интервале длин волн [ ), которую в дальнейшем будем именовать просто аппаратной функцией. Если интенсивность излучения в интервале длин волн [ 1, 1,  2] меняется слабо, то влияние особенностей прибора на процессы ее измерения можно вообще не учитывать. 2] меняется слабо, то влияние особенностей прибора на процессы ее измерения можно вообще не учитывать.
При измерениях полусферических потоков солнечной радиации помимо функции f ( ( ) важную роль играет функция f ) важную роль играет функция f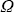 ( ( , ,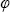 ), поскольку интенсивность на входе прибора теперь очевидно меняется по направлениям ( ), поскольку интенсивность на входе прибора теперь очевидно меняется по направлениям ( , ,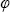 ). Но, сравнивая выражения (1.1.4) и (1.1.11) легко видеть, что для измерения именно величины потока солнечного излучения необходимо выполнения условия . Это требование к приборам, измеряющим потоки солнечного излучения, называется “косинусной зависимостью”. ). Но, сравнивая выражения (1.1.4) и (1.1.11) легко видеть, что для измерения именно величины потока солнечного излучения необходимо выполнения условия . Это требование к приборам, измеряющим потоки солнечного излучения, называется “косинусной зависимостью”.
1 Заметим, что, во-первых, монохроматическое излучение в принципе невозможно. Это следует из чисто математических свойств преобразования Фурье: спектр, состоящий из одной частоты, возможен лишь для сигнала бесконечного по времени. Во-вторых, для монохроматических пучков не может выполняться принцип независимости, поскольку они всегда интерферируют . Однако оба эти противоречия можно снять, если рассматривать монохроматическое излучение не как физический, а как математический объект – результат разложения реального излучения на сумму (интеграл Фурье) гармонических составляющих. Отдельная составляющая такого разложения и интерпретируется как монохроматическое излучение. |