Основной задачей выполнявшихся самолетных измерений интенсивности излучения в атмосфере было исследование спектральных отражательных свойств подстилающих поверхностей. Как показано в разделе 1.4, отражательные характеристики поверхности описываются функцией R(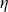 , , , ,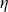 ', ', '), определяемой из соотношений между интенсивностями падающего на поверхность и отраженного излучения по формуле (1.4.3). Простейшая характеристика поверхности – альбедо определяется как отношение восходящего и нисходящего потоков солнечной радиации (1.4.1) (см сноску в разделе 1.4 на стр. 56) . '), определяемой из соотношений между интенсивностями падающего на поверхность и отраженного излучения по формуле (1.4.3). Простейшая характеристика поверхности – альбедо определяется как отношение восходящего и нисходящего потоков солнечной радиации (1.4.1) (см сноску в разделе 1.4 на стр. 56) .
Тем не менее, учитывая то обстоятельство, что в безоблачной атмосфере вклад многократно отраженного излучения в нисходящий поток невелик (оценки его будут получены в гл. 6), принято считать, что экспериментально измеренные отражательные характеристики с хорошим приближением соответствуют теоретическим. Наблюдается, однако, зависимость их от соотношения в нисходящем потоке прямого и рассеянного излучения , особенно существенная при сравнении результатов, полученных в безоблачной атмосфере и при сплошной облачности.
В силу наличия диффузного отражения (см. раздел 1.4), также невозможно измерить функцию четырех аргументов R(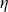 , , , ,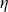 ', ', ') для поля солнечного излучения, поскольку реально измеряемая интенсивность в направлении ( ') для поля солнечного излучения, поскольку реально измеряемая интенсивность в направлении (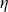 , , ) зависит сразу от всего поля падающего на поверхность излучения (см. определение оператора отражения формулой (1.4.3)). Поэтому максимально информативная характеристика отражения, которую удается получать из натурных измерений, – это коэффициент спектральной яркости (КСЯ), который определяется выражением: ) зависит сразу от всего поля падающего на поверхность излучения (см. определение оператора отражения формулой (1.4.3)). Поэтому максимально информативная характеристика отражения, которую удается получать из натурных измерений, – это коэффициент спектральной яркости (КСЯ), который определяется выражением:
где 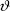 – угол визирования (надир – – угол визирования (надир – 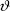 = 0), = 0),  – азимут визирования (в направлении “на Солнце” – азимут визирования (в направлении “на Солнце”  =0), I( =0), I(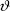 , , ) – интенсивность излучения, отраженного от поверхности, и I0 – интенсивность излучения, отраженного от абсолютно белой ортотропной поверхности. ) – интенсивность излучения, отраженного от поверхности, и I0 – интенсивность излучения, отраженного от абсолютно белой ортотропной поверхности.
Во время полета самолета технически невозможно выполнять непосредственные измерения величины I0, поэтому реально измерения КСЯ проводились по следующей схеме. В наземных условиях, с применением той же аппаратуры измерялась интенсивность I0 и, одновременно с помощью второго прибора измерялся поток нисходящего излучения F0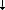 . В качестве ортотропной белой поверхности использовалась алюминиевая подложка покрытая оксидом магния, полученным от сжигания магниевой стружки непосредственно перед измерениями. Альбедо такого экрана принималось равным 0,97. Результатом этих наземных измерений было получение калибровочной кривой . В качестве ортотропной белой поверхности использовалась алюминиевая подложка покрытая оксидом магния, полученным от сжигания магниевой стружки непосредственно перед измерениями. Альбедо такого экрана принималось равным 0,97. Результатом этих наземных измерений было получение калибровочной кривой 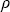 = 0,97F0 = 0,97F0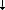 /I0. Заметим, что теоретически из определения альбедо по формуле (1.4.1) и выражения восходящего потока через интенсивность I0 по формуле (1.1.4) следует, что для абсолютно белой ортотропной поверхности /I0. Заметим, что теоретически из определения альбедо по формуле (1.4.1) и выражения восходящего потока через интенсивность I0 по формуле (1.1.4) следует, что для абсолютно белой ортотропной поверхности 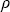 = =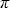 . Во время самолетных измерений КСЯ одновременно (двумя приборами) регистрировались величины нисходящего потока F . Во время самолетных измерений КСЯ одновременно (двумя приборами) регистрировались величины нисходящего потока F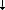 и отраженной от поверхности интенсивности I( и отраженной от поверхности интенсивности I(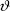 , , ). КСЯ согласно (3.4.1) вычислялся как ). КСЯ согласно (3.4.1) вычислялся как
Выражая I(J, j) из (3.4.2) с учетом упомянутых выше соотношений (1.1.4) и (1.4.1) получаем формулу теоретической связи между КСЯ и альбедо поверхности :
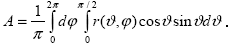 |
(3.4.3) |
Аппаратура для выполнения измерений и оценка точности измерений описаны в разделе 3.1. Однако для получения величин КСЯ, учитывая, что измерения интенсивностей и потоков выполнялись двумя различными приборами, операция деления (3.4.2) приводит к появлению дополнительной погрешности, связанной со случайным смещением шкалы длин волн одного прибора относительно другого (табл.3.1). Когда величина сигнала меняется по спектру слабо, эффект этого смещения несущественен, но в тех участках спектра где наблюдается быстрое изменение сигнала, например в полосе поглощения кислорода 760 нм, погрешность определения КСЯ может резко возрастать.
Наличие в полученных по формулам (3.4.2) величинах КСЯ случайных погрешностей, обусловленных факторами полета и особенно неоднородностью поверхности, проявляется в спектрах КСЯ в виде быстрых случайных осцилляций. Для их фильтрации использовалась процедура сглаживания с треугольной весовой функцией приведенная в работе , приводящая к формулам :
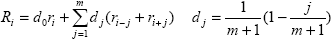 |
(3.4.4) |
где ri – исходный и Ri – сглаженный спектры КСЯ, индекс i соответствует номеру точки в спектре, m – полуширина сглаживания, конкретно использовалась m = 9. Заметим, что полуширина сглаживания m в (3.4.4) – это параметр частотной фильтрации данных , она никак не связана с полушириной аппаратной функции прибора (3.1.1). Для дальнейшего анализа использовались только сглаженные спектры КСЯ. Учитывая полуширину сглаживания, а также сужение спектрального диапазона сглаженных данных и значительную погрешность результатов измерений на краях спектрального диапазона прибора, спектры КСЯ рассматривались в интервале 350 ‑ 850 нм с шагом 10 нм [16-18].
Если рассматривать КСЯ как отражательную характеристику только подстилающей поверхности, а не всей системы “атмосфера плюс поверхность”, необходимо максимально снизить влияние на КСЯ слоя атмосферы между самолетом и поверхностью, для чего, казалось бы, следует проводить измерения на минимальных высотах. Однако с уменьшением высоты полета увеличивается «болтанка» и растет вклад обусловленной ею случайной составляющей в суммарную погрешность определения КСЯ. Поэтому необходимо было выбрать оптимальные высоты полетов, при которых эффекты влияния слоя атмосферы на КСЯ оставались бы относительно незначительными а «болтанка» не становилась основным фактором, определяющим погрешность измерений. По опыту полетов на самолете ИЛ-14 в качестве таких оптимальных высот были выбраны 200 ‑ 300 м над водной поверхностью и 300 ‑ 500 м над сушей. Однако, по различным причинам, иногда приходилось выполнять измерения и на высотах, отличных от оптимальных. Следует отметить, что существует методика, позволяющая исключать влияние атмосферы на КСЯ [7,45] для чего требуется проводить измерения высотных профилей КСЯ. Такие измерения в ходе рассматриваемых экспериментов также проводились, однако их доля в общем массиве данных невелика, поэтому, на первом этапе авторы ограничились анализом КСЯ, измеренных на высотах от 500 м и ниже , , . Подчеркнем, что, даже работая на малых высотах, полностью исключить искажающее влияние атмосферы на КСЯ невозможно. Оно, например, проявляется в завышении значений КСЯ в УФ области спектра, вызванного сильным молекулярным рассеянием света (1.2.14), и в занижении значений в полосах поглощения кислорода и водяного пара в ИК области.
При анализе полученных величин КСЯ, наибольший интерес представляет изучение зависимостей их спектров от типа поверхности, направления визирования, зенитного угла Солнца и т.п. Учитывая значимость случайной составляющей погрешности измерения КСЯ, констатация наличия, либо отсутствия зависимостей спектров от указанных факторов возможна лишь после статистической обработки массива данных измерений КСЯ. Поскольку факторы, влияющие на результаты определения КСЯ, весьма многочисленны и сильно изменчивы в процессе измерений (например, зенитный угол Солнца меняется непрерывно), применение стандартной и простейшей статистической методики усреднения данных, полученных при одинаковых условиях, в данном случае невозможно просто потому, что нельзя приписать достаточно большим группам спектров указанные одинаковые условия измерений.
С целью преодоления этих трудностей при анализе данных был применен кластерный анализ – метод формальной классификации спектров КСЯ. Суть его заключается в разбиении всей совокупности спектров КСЯ на классы (или группы, кластеры) , , причем спектры объединяются в классы без учета какой-либо априорной информации о них, а только по принципу “близости”. Таким образом, кластерный анализ сводит задачу изучения зависимостей спектров КСЯ от многих указанных выше факторов к описанию особенностей сравнительно небольшого числа классов. В качестве численной характеристики “близости” спектров используется функция метрики – расстояния между двумя классифицируемыми объектами , . Алгоритм классификации строится рекуррентно: пусть некоторые спектры (на старте рекурсии – один) уже выделены в класс; следующий спектр добавляется в тот же класс, если расстояние от него до выделенного класса меньше некоторого заданного; после того, как добавляемых спектров не остается, процедура классификации повторяется для всех оставшихся (не вошедших в класс) спектров и т.д. вплоть до исчерпания всей совокупности классифицируемых спектров.
В работах , приведено достаточное количество различных функций, удовлетворяющих аксиоматическим требованиям к метрике . Заметим, что применение различных метрик приводит, вообще говоря, к разным итогам классификации, поэтому выбор метрики следует делать, исходя из условий конкретной задачи. Эти условия, как отмечено в , нередко оказываются такими, что математически корректные метрики , им не удовлетворяют. В этом случае используются различные эвристические метрики , не являющиеся метриками в строгом смысле слова. Мы были вынуждены также пойти по этому пути, и использовали в качестве меры расстояния между двумя спектрами R(1) и R(2) функцию
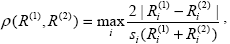 |
(3.4.5) |
где si – относительное случайное СКО измеренных КСЯ (конкретные значения – см. [16-18]). В (3.4.5) учитываются различия между спектрами на каждой длине волны (а не на всех в среднем), поскольку существенной для классификации может оказаться даже разница в спектрах на узком интервале длин волн. Особенно это важно для выявления сбойных спектров, о чем пойдет речь ниже. Разница значений спектров в (3.4.5) для перехода к относительным величинам нормируется на их среднее арифметическое, а для учета различной по спектру погрешности – еще и на СКО. В качестве расстояния от спектра до класса использовалось расстояние до стартового спектра класса. Спектр зачислялся в класс, если это расстояние было менее трех, т.е. по стандартному статистическому правилу “допустимое отклонение от среднего не более трех СКО”.
Выбор стартового спектра классификации (следовательно, рекуррентно и стартового спектра каждого последующего класса) также является весьма неопределенным моментом кластерного анализа. Проблема заключается в том, что этот спектр должен соответствовать максимуму многомерной функции распределения (гистограммы) совокупности классифицируемых объектов, а поиск такого максимума является сложной математической и вычислительной задачей. На основе анализа применимости в нашей конкретной задаче классификации КСЯ различных методов поиска стартового спектра, обзор которых приведен в , был выбран следующий алгоритм. Каждый спектр, подлежащей классификации совокупности, проверялся на возможность использования в качестве стартового. Для него определялось число спектров, попадающих с ним в один класс, среднее расстояние, выражаемое формулой (3.5.5), до таких спектров и отношение среднего расстояния к числу спектров. Последняя величина, очевидно, имеет смысл плотности спектров в классе. В качестве стартового выбирался спектр, которому соответствует максимальная плотность.
После формальной, машинной, классификации необходим этап “ручного” анализа ее результатов (очень убедительное обоснование этой необходимости дано в предисловии к русскому изданию монографии на этом этапе уже анализировалась информация о факторах измерений для каждого из полученных классов, некоторые классы по результатам такого анализа объединялись. Важным и, на наш взгляд, могущим иметь широкое практическое применение при оперативной обработке результатов измерений радиационных характеристик атмосферы и поверхности результатом кластерного анализа является фактически автоматическое обнаружение “сбойных” спектров. Действительно, если класс состоит из единственного спектра, а по условиям измерений этот спектр не должен как-то выделяться среди других, есть серьезные основания считать его “сбойным”.
После завершения процедуры классификации, для каждого класса по совокупности входящих в него спектров вычислялось среднее значение и СКО. Заметим, что при этом СКО иногда оказывалось и меньше исходного случайного СКО si. Это, очевидно, объясняется статистическим усреднением спектров, а также тем, что, например, вклад в СКО погрешности, связанной с неоднородностью поверхности для реальных условий измерений мог быть и меньше средней оценки, приведенной в табл. 3.1.
Результаты проведенной классификации подробно обсуждаются в работах , , . Проиллюстрируем характерные спектры КСЯ для основных природных подстилающих поверхностей на рис. 3.17. На рисунке, в частности, представлены КСЯ для трех типов поверхности, над которыми выполнялись зондировки: снег, песок и чистая озерная вода. При этом заметим, что в приближении ортотропной поверхности, согласно определению (3.5.1), альбедо поверхности равно КСЯ. Рассмотрим, однако, насколько для указанных поверхностей справедливо такое приближение. По результатам проведенной классификации при измерениях над снежной поверхностью, зависимость КСЯ от направления визирования не обнаружена, т.е. снежный покров по своим отражательным свойствам близок к ортотропной поверхности. Точность приближения определяется СКО класса “снег” и составляет в относительных величинах в среднем по спектру 8% , , . В Приложении 1 представлены описания основных классов КСЯ и приведены спектральные значения в табл. 1.4 – 1.7.
Водная поверхность является наиболее анизотропной из всех природных поверхностей. Это иллюстрирует рис. 3.18. В направлении визирования “на Солнце” ( = 0°) имеется резкий максимум – “солнечная дорожка”, сформированная зеркально отраженными от взволнованной водной поверхности солнечными лучами (кривые 2-3 на рис. 3.18). В противоположном направлении имеется слабый минимум отражения (кривая 4) объяснение которому можно найти в работе [53]. К сожалению, для песка мы не имели возможности измерить зависимости КСЯ от угла и азимута визирования. Однако визуально было четко видно, что песок является обратно отражающей поверхностью (см. раздел 1.4). Поскольку подобными свойствами обладает и поверхность мохового болота (качественно картины анизотропии для песка и болота близки), данные рис. 3.19, полученные при измерениях над болотом позволяют оценить аналогичную зависимость КСЯ от угла и азимута визирования для песчаной поверхности. Хорошо видно увеличение КСЯ при приближении к противосолнечной точке ( = 0°) имеется резкий максимум – “солнечная дорожка”, сформированная зеркально отраженными от взволнованной водной поверхности солнечными лучами (кривые 2-3 на рис. 3.18). В противоположном направлении имеется слабый минимум отражения (кривая 4) объяснение которому можно найти в работе [53]. К сожалению, для песка мы не имели возможности измерить зависимости КСЯ от угла и азимута визирования. Однако визуально было четко видно, что песок является обратно отражающей поверхностью (см. раздел 1.4). Поскольку подобными свойствами обладает и поверхность мохового болота (качественно картины анизотропии для песка и болота близки), данные рис. 3.19, полученные при измерениях над болотом позволяют оценить аналогичную зависимость КСЯ от угла и азимута визирования для песчаной поверхности. Хорошо видно увеличение КСЯ при приближении к противосолнечной точке ( = 180°), где его значение в 1,5 – 2 раза больше, чем в надире. = 180°), где его значение в 1,5 – 2 раза больше, чем в надире.
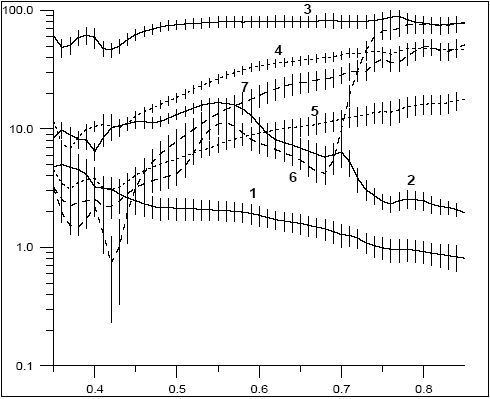
Рисунок 3.17. КСЯ характерных природных поверхностей. Приведены средние значения КСЯ соответствующих классов и интервал в 1 СКО: 1 – чистая озерная вода с низким содержанием хлорофилла и минеральных взвесей; 2 – озерная вода с высоким содержанием хлорофилла и минеральных взвесей; 3 – снег; 4 – песок; 5 – почва (чернозем); 6 – зеленая растительность (трава); 7 – желтая растительность (спелые зерновые). 2 3 1 4
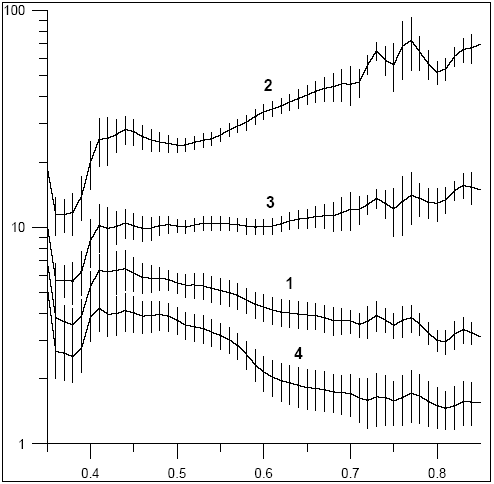
Рисунок 3.18. Зависимость КСЯ водной поверхности от направления визирования. Приведены средние значения КСЯ соответствующих классов и интервал в 1 СКО: 1 – надир; 2 – направление зеркального отражения; 3 – угол, соответствующий зеркальному отражению на азимуте 45°; 4 – этот же угол на азимуте 180°
Для аналитического описания анизотропии отражения на основе полученных данных по измеренным значениям КСЯ введем функцию вида
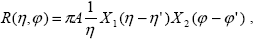 |
(3.4.6) |
где A – альбедо поверхности, (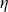 ', ', ') – некоторое выделенное направление отражения, конкретно – направление зеркального, либо обратного отражения, X1( ') – некоторое выделенное направление отражения, конкретно – направление зеркального, либо обратного отражения, X1(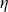 '') и X2( '') и X2( '') – некоторые функции, описывающие анизотропию при отклонении косинуса угла отражения '') – некоторые функции, описывающие анизотропию при отклонении косинуса угла отражения 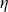 и азимута отражения j от выделенного направления: и азимута отражения j от выделенного направления: 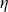 ''= ''=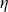 – – 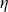 ', ',  ''= ''= – –  '. Множитель '. Множитель 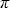 / /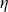 возникает из необходимости согласования (3.4.6) с выражением альбедо через КСЯ (3.4.3). Из этого же соотношения для функций X1( возникает из необходимости согласования (3.4.6) с выражением альбедо через КСЯ (3.4.3). Из этого же соотношения для функций X1(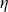 '') и X2( '') и X2( '') получаются следующие условия нормировки: '') получаются следующие условия нормировки:
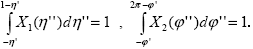 |
(3.4.7) |
Условия (3.4.7) фактически однотипны, поэтому функции X1(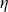 '')и X2( '')и X2( '') можно строить на основе одного аналитического выражения. Заметим также, что эти функции по смыслу их введения должны достигать максимумов при '') можно строить на основе одного аналитического выражения. Заметим также, что эти функции по смыслу их введения должны достигать максимумов при 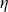 = = 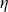 ', ',  = =  ', т.е. при ', т.е. при 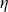 ''= 0, ''= 0,  ''= 0, а для остальных значений описывать убывание отражения. Но всем указанным условиям удовлетворяет классическая функция Хэньи-Гринстейна определенная формулой (1.2.20), которая широко известна, весьма удобна при применении в теории переноса излучения (см. раздел 1.3), и для которой элементарно вычисляются интегралы вида (3.4.7). Поэтому на основе функции Хэньи-Гринстейна предлагается аппроксимация ''= 0, а для остальных значений описывать убывание отражения. Но всем указанным условиям удовлетворяет классическая функция Хэньи-Гринстейна определенная формулой (1.2.20), которая широко известна, весьма удобна при применении в теории переноса излучения (см. раздел 1.3), и для которой элементарно вычисляются интегралы вида (3.4.7). Поэтому на основе функции Хэньи-Гринстейна предлагается аппроксимация
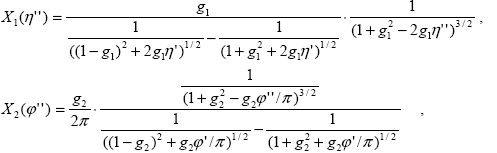 |
(3.4.8) |
где 0 < g1 < 1 и 0 < g2 < 1 – параметры аппроксимации.
Для общей оценки точности предлагаемой аппроксимации (3.4.6) и (3.4.8), а также для получения оценок ее конкретных параметров были найдены величины A, g1 и g2 простым перебором на компьютере возможных их значений по всем измерениям КСЯ (исходным, а не результатам классификации). Процесс проводился для соответствующих данных по воде и моховому болоту с выбором конкретных значений параметров, обеспечивающих минимальное СКО аппроксимации. Поскольку при измерениях угол визирования не превышал 45° (см. раздел 3.1), полученные значения A в (3.4.6) лишены физического смысла (это не альбедо, а просто некий коэффициент). Что же касается параметров анизотропии, то для воды получены g1 = 0,7 и g2 = 0,7 для мохового болота: g1 = 0,2 и g2 = 0,5.
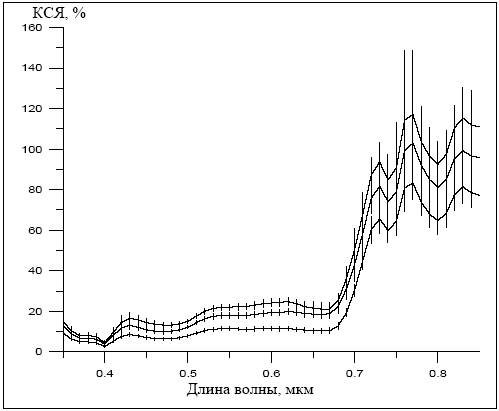
3.19. Зависимость КСЯ мохового болота от направления визирования. Приведены средние значения КСЯ соответствующих классов и интервал в 1 СКО: верхняя кривая – направление обратного отражения: средняя кривая – угол, соответствующий обратному отражению на азимуте 135°; нижняя кривая – надир и азимуты визирования от 0 до 90°.
Заметим, что сетка измерений по углу и азимуту была не слишком подробной [16-18], поэтому точность полученных коэффициентов невелика, их можно считать лишь грубой оценкой, приняв их СКО равным 0,05. По этой же причине можно не принимать во внимание спектральный ход коэффициентов g1 и g2 (рост от УФ к БИК диапазону) и приписать всем длинам волн одинаковые их значения. Интересно отметить, что формально вычисленное СКО аппроксимации (3.4.6) и (3.4.8) оказывается порядка 10%, т.е. близким к точности измерений КСЯ. Поэтому можно сделать вывод, что формулы (3.4.6), (3.4.8) достаточно хорошо описывает анизотропию реальных поверхностей, хотя, оговоримся еще раз, столь малое СКО может быть лишь следствием небольшого числа точек в сетке измерений по углу и азимуту |