Измерения спектральных потоков солнечной радиации проводились с целью вычисления лучистых притоков, что и обусловило как схему измерений, так и методику обработки результатов. Здесь следует выделить два существенно различных случая: измерения в условиях сплошной слоистообразной облачности и измерения в условиях безоблачной атмосферы. Для получения сопоставимых результатов, измерения как нисходящих, так и восходящих потоков выполнялись с использованием одного прибора (через верхнее и нижнее молочные стекла световода).
В случае сплошной облачности измерения потоков солнечной радиации выполнялись вне облака: выше верхней и ниже нижней его границы и внутри облака с шагом по высоте 100 м. Поскольку проведение эксперимента в условиях облачной атмосферы требует как высокой степени горизонтальной однородности облака, так и стабильности этой однородности во времени, измерения выполнялись максимально быстро, по одной паре потоков (нисходящий и восходящий) на каждой высоте. При этом, как правило, удавалось выполнить лишь один подобный цикл измерений. Подчеркнем, что случаи достаточно однородной по горизонтали и стабильной во времени слоистой облачности крайне редки, поэтому данных измерений в облачных условиях существенно меньше, чем в безоблачных.
Основной составляющей погрешности при измерениях потоков в условиях сплошной облачности является случайная погрешность, вызванная неравномерностью освещения (табл. 3.1). Для измерений на разных высотах она приводит к “пилообразным” искажениям высотного профиля (рис. 3.2). Отфильтровать эти высокочастотные искажения можно с применением процедур сглаживания, см., например, монографию , однако их стандартные алгоритмы , в данном случае оказались неэффективны, и пришлось разработать специальную методику .
Процедура сглаживания искажений спектральных значений потоков солнечной радиации для восходящего и нисходящего потоков проводится заменой значения потока в точке кривой на каждом высотном уровне средним взвешенным значением потока в этой точке и в двух соседних (сверху и снизу)
 |
(3.2.1) |
где 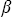 j – веса сглаживания (общие для всех длин волн, высот и типов потоков), f j – веса сглаживания (общие для всех длин волн, высот и типов потоков), f (zi), f (zi), f 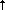 (zi) – результаты измерений нисходящих и восходящих потоков на высоте zi, F (zi) – результаты измерений нисходящих и восходящих потоков на высоте zi, F (zi), F (zi), F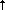 (zi) – значения потоков, рассчитанные в ходе вторичной обработки результатов измерений. Веса (zi) – значения потоков, рассчитанные в ходе вторичной обработки результатов измерений. Веса 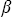 j в выражении (3.2.1) находились из требований выполнения законов физики. j в выражении (3.2.1) находились из требований выполнения законов физики.
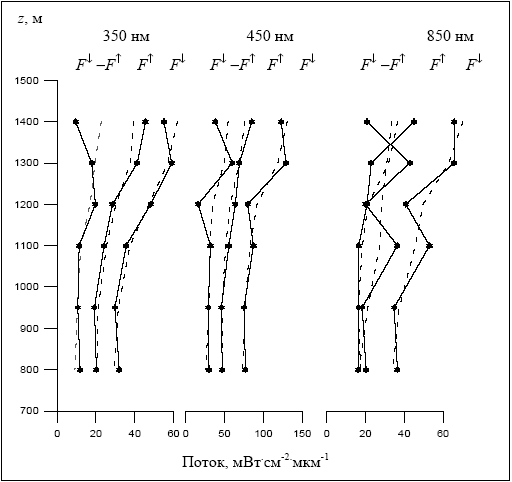
Рисунок 3.2. Вертикальные профили полного, исходящего и восходящего потоков солнечного излучения в облаке для трех длин волн. Сплошные кривые – исходные измерения, пунктирные – сглаженные значения. Измерения 20.04.1985, сплошная слоистая облачность, верхняя граница 1400 м, нижняя – 900 м, зенитный угол Солнца J0 = 49° (z = 0,647), подстилающая поверхность – снег.
Поскольку лучистый приток в слоях атмосферы не может быть отрицательным, полный поток не должен возрастать с ростом оптической глубины (см. раздел 1.1). Иными словами для результатов выражений (3.2.1) должно выполняться условие
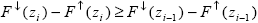 |
(3.2.2) |
Подстановка (3.2.2) в (3.2.1) приводит к условиям для нахождения весов bj
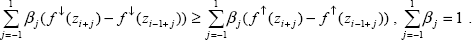 |
(3.2.3) |
Система уравнений (3.2.3) решалась итерационным методом. Сначала при замене в (3.2.3) неравенства строгим равенством находились значения bj для измеренных потоков f (zi), f (zi), f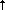 (zi), причем для согласования сглаживания на соседних длинах волн рассматривались лишь три длины волны в центрах УФ (370 нм), ВД (550 нм) и БИК (850 нм) диапазонов. Полученная система (3.2.3) решалась известным методом наименьших квадратов (МНК) , . Конкретные формулы МНК и его особенности будут рассмотрены в 4-ой главе, а в этом разделе договоримся приводить лишь полученные результаты. Затем с помощью соотношений (3.2.1) вычислялись F (zi), причем для согласования сглаживания на соседних длинах волн рассматривались лишь три длины волны в центрах УФ (370 нм), ВД (550 нм) и БИК (850 нм) диапазонов. Полученная система (3.2.3) решалась известным методом наименьших квадратов (МНК) , . Конкретные формулы МНК и его особенности будут рассмотрены в 4-ой главе, а в этом разделе договоримся приводить лишь полученные результаты. Затем с помощью соотношений (3.2.1) вычислялись F (zi), F (zi), F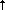 (zi) и проверялось выполнение условий (3.2.2) для всех длин волн и высот. В случае выполнения условий итерации заканчивались, иначе – описанная выше процедура повторялась уже с заменой в (3.2.3) значений f (zi) и проверялось выполнение условий (3.2.2) для всех длин волн и высот. В случае выполнения условий итерации заканчивались, иначе – описанная выше процедура повторялась уже с заменой в (3.2.3) значений f (zi), f (zi), f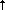 (zi) на найденные F (zi) на найденные F (zi), F (zi), F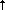 (zi) и т.д. При этом добавлялось еще одно физическое ограничение: отклонение значений F (zi) и т.д. При этом добавлялось еще одно физическое ограничение: отклонение значений F (zi), F (zi), F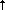 (zi) от измеренных значений f (zi) от измеренных значений f (zi), f (zi), f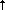 (zi) (от результатов измерений) на любой из итераций не может превышать среднеквадратической случайной погрешности измерений (10%, табл. 3.1). Заметим, что обычно для получения окончательных значений F (zi) (от результатов измерений) на любой из итераций не может превышать среднеквадратической случайной погрешности измерений (10%, табл. 3.1). Заметим, что обычно для получения окончательных значений F (zi) и F (zi) и F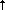 (zi) было достаточно двух - трех итераций. Пример результатов описанной процедуры сглаживания приведен на рис.3.2. (zi) было достаточно двух - трех итераций. Пример результатов описанной процедуры сглаживания приведен на рис.3.2.
Полученные по описанной выше методике значения потоков F (zi) и F (zi) и F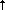 (zi) для условий сплошной облачности были окончательными результатами вторичной обработки результатов измерений. За их случайную погрешность принималось среднеквадратическое отклонение сглаженного профиля от исходного. Следует отметить, что в суммарную погрешность результатов значительный вклад вносит систематическая погрешность калибровки (см. табл. 3.1), однако при использовании методов дальнейшей обработки и интерпретации результатов, которые будут приведены в гл.6, потоки солнечной радиации учитываются в виде безразмерных комбинаций, следовательно, погрешность калибровки может не приниматься во внимание. Заметим также, что в силу быстрого проведения самолетного эксперимента в облаке, зенитный угол Солнца в процессе измерений менялся несущественно (на 1–2°) и при обработке результатов им приписано единое значение зенитного угла Солнца. (zi) для условий сплошной облачности были окончательными результатами вторичной обработки результатов измерений. За их случайную погрешность принималось среднеквадратическое отклонение сглаженного профиля от исходного. Следует отметить, что в суммарную погрешность результатов значительный вклад вносит систематическая погрешность калибровки (см. табл. 3.1), однако при использовании методов дальнейшей обработки и интерпретации результатов, которые будут приведены в гл.6, потоки солнечной радиации учитываются в виде безразмерных комбинаций, следовательно, погрешность калибровки может не приниматься во внимание. Заметим также, что в силу быстрого проведения самолетного эксперимента в облаке, зенитный угол Солнца в процессе измерений менялся несущественно (на 1–2°) и при обработке результатов им приписано единое значение зенитного угла Солнца.
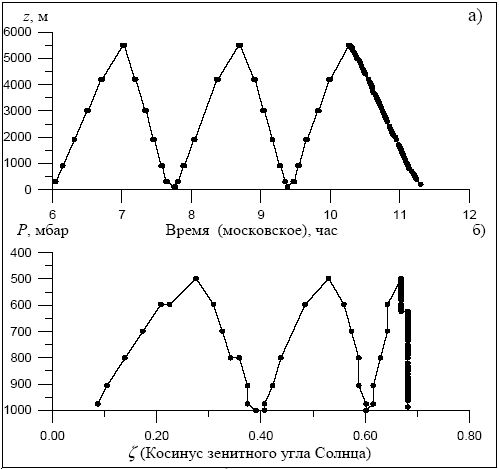
Рисунок 3.3. Схема зондировки: а) – в координатах “время-высота”, б) – в координатах “косинус зенитного угла Солнца - давление”. Измерения 14.10.1983 над пустыней Кара-Кум, точками показаны высоты измерений
При измерениях в безоблачной атмосфере представляет интерес сравнение измеренных потоков с внеатмосферным спектром Солнца. В качестве простейшего обоснования этого подхода можно сослаться на закон Бугера (1.3.11), если, например, мы хотим из данных измерений определить оптическую глубину атмосферы. Непосредственно измерить внеатмосферный нисходящий поток солнечного излучения с борта самолета невозможно, поэтому при измерениях в условиях безоблачной атмосферы вклад систематической погрешности калибровки прибора существенен.
При отсутствии облачности в силу слабого поглощения солнечной радиации в атмосфере значения спектральных лучистых притоков очень малы, а случайные погрешности результатов измерений потоков, связанные с «самолетными» факторами, неприемлемо велики (до 10%). Поэтому основными задачами на этапе планирования эксперимента и обработки результатов измерений являлись минимизация случайной погрешности результатов и коррекция систематической погрешности калибровки измерительного прибора.
Очевидно, что повышение точности измерений спектрометра само по себе важно, но погрешность измерений с борта самолета, обусловленная факторами полета, состояния атмосферы и неоднородностью подстилающей поверхности, не зависит от экспериментатора и может достигать высоких значений. Поэтому единственным способом получения высокоточных результатов эксперимента является применение наиболее адекватных методов статистической обработки данных измерений. Если под статистической обработкой понимать ее простейший вариант – усреднение данных, то для получения вертикальных профилей нисходящих и восходящих потоков следовало бы измерять несколько спектров на каждой высоте. Но тогда измерения займут продолжительное время и потоки на разных высотах будут получены при существенно разных зенитных углах Солнца, что очень осложнит их дальнейшую интерпретацию.
Учитывая это обстоятельство, О.Б. Васильевым была разработана специальная схема проведения измерений, получившая название “зондировка” , . Идея зондировки – выполнение подробных измерений профилей потоков при минимальном изменении зенитного угла Солнца для последующего получения зависимости потоков от высоты, и использовании измеренных на предварительных подъемах и спусках значений потоков для коррекции изменений зенитного угла Солнца во время подробного спуска. В соответствии с этой схемой выполнялись два или три подъема и спуска от 50 м (1000 мбар) до 5600 м (500 мбар) с измерениями через 100 мбар и подробный спуск в районе местного полдня (при минимальном изменении зенитного угла Солнца) с 5600 м до 50 м с измерениями через 100 м (рис.3.2.а). Минимальная высота измерений (50 м) обусловлена нормативными требованиями безопасности полетов, максимальная (5600 м) – техническими возможностями самолета ИЛ-14. При полете на оптимальных режимах удавалось выполнять только два подъема и спуска, однако в большинстве случаев экипажи самолета активно помогали выполнению измерений, соглашаясь летать с предельно допустимыми вертикальными скоростями, что позволяло выполнять по три подъема и спуска.
При зондировках менялась высота полета, однако, при дальнейшей обработке результатов измерений вместо шкалы высот использовали шкалу давлений воздуха (рис.3.3 б). Это связано со следующими обстоятельствами. На высотах более 500 м при измерениях использовалась авиационная абсолютная высота – высота, измеряемая по альтиметру, относительно уровня 760 мм.рт.ст., т.е. фактически давление воздуха, выраженное в единицах высоты согласно шкале стандартной модели атмосферы . Точность приборного измерения абсолютной высоты составляет 50 м, но при работе в условиях жесткого дефицита времени пилотам сложно было точно занимать конкретные высоты при измерениях, поэтому реальную погрешность высотной привязки будем считать равной 100 м. На высотах ниже 500 м использовалась авиационная истинная высота – расстояние от самолета до поверхности Земли, измеряемое с высокой точностью по радиовысотомеру. Между этими двумя высотными шкалами имеется скачок, связанный с высотой земной поверхности над уровнем моря и отличием профиля давления в реальной атмосфере от стандартной модели . Этот скачок определялся путем сравнения показаний альтиметра и радиовысотомера и учитывался при формировании общей высотной шкалы (по давлению) для измеренных профилей потоков.
Для выполнения зондировок были выбраны акватория Ладожского озера и пустыня Кара-Кум (Туркмения, район пос. Репетек). Выбор обусловлен отмеченными в предыдущем разделе требованиями большой пространственной однородности поверхности и наличием вблизи аэропортов. Соответственно зондировки выполнялись над тремя типами подстилающей поверхности: снег (на льду Ладожского озера), вода (Ладожское озеро) и песок (пустыня Кара-Кум).
Начальным, и, как ни странно, наиболее сложным этапом вторичной обработки зондировок оказался предварительный анализ и коррекция спектров потоков. Это было связано, прежде всего, с весьма сложными условиями полетов, при которых работа аппаратуры на борту самолета приводила к сбоям при измерении спектров – получению искаженных значений на отдельных длинах волн. Однако в связи с большой научной ценностью каждого спектра (и большой стоимостью экспериментов) исключать из дальнейшей обработки весь спектр из-за наличия сбоев на одной или нескольких длинах волн представлялось неоправданным. Это потребовало проведения тщательного анализа сбоев и корректировки спектров. Кроме того, условия полетов не позволяли реализовать в полном объеме идеальную схему зондировки, описанную выше, что вызвало необходимость корректировки данных с учетом отклонений процедуры измерений от идеальной схемы.
Попытки создать полностью автоматизированный алгоритм коррекции сбоев в измеренных спектрах оказались неудачными из‑за огромного разнообразия конкретных проявлений сбоев. Они могли быть выявлены и устранены лишь в ручном режиме с использованием средств визуализации описанной в предыдущем разделе базы данных полученных спектров. Для измерений в условиях сплошной облачности именно так и было сделано. Однако, учитывая что количество зондировок и измеренных спектров, полученных в условиях безоблачной атмосферы было намного больше, чем для облачной, такой подход требовал слишком больших затрат времени и сил. Именно это обстоятельство и является основной причиной того, что значительный массив данных измерений, выполненных в 1983‑1985 годах, был обработан лишь в конце 1990-х, когда удалось создать систему оперативной обработки. В основу этой системы положена идея реализации полуавтоматического режима. Анализ данных проводился автоматически, но при обнаружении сбоев, осуществлялся переход на ручную обработку в интерактивном визуальном режиме, при этом автоматика “подсказывала” оператору возможные варианты решения.
Ниже приведено краткое описание предложенной системы оперативной обработки спектров с более подробным изложением подходов и схем, которые могут найти широкое применение в практике предварительного анализа результатов измерений потоков и интенсивностей солнечной радиации в атмосфере.
На первом этапе путем логического анализа каждого спектра устранялись сбои типа “выбросов” и нестыковки диапазонов. Выброс – это сбой, при котором на одной или нескольких расположенных рядом длинах волн значения спектра резко отличаются по величине от соседних точек. Они идентифицируются по превышению относительной разности двух следующих подряд значений спектра определенной величины (конкретно на 10%). Следует отметить при этом, что необходимо использовать достаточно обстоятельный логический анализ, чтобы не принять за выброс сильную полосу поглощения, и учесть все возможные варианты расположения выбросов в начале или конце спектра, а также вблизи друг от друга. Коррекция выбросов заключается в замене точек сбоев на интерполированные точки, рассчитанные по соседним “правильным” значениям. После устранения сбоев процедура повторяется (поскольку сильные выбросы могут “маскировать” более слабые) до тех пор, пока на очередной итерации не будет обнаружено ни одного выброса. Нестыковки, т.е. скачки на границах УФ – ВД и ВД – БИК диапазонов спектра связаны с измерениями в разных диапазонах разными ФЭУ (см. п.3.1). Причина их появления, несмотря на все ухищрения первичной обработки, вероятно, обусловлена отклонениями динамической характеристики ФЭУ от линейной. Устранение нестыковок проводилось путем прибавления к УФ и БИК частям спектра соответствующих константных корректирующих значений.
Выявление сбоев путем логического анализа формы отдельного спектра на самом деле не слишком эффективно. Действительно, при визуальном анализе спектров, оператор с легкостью идентифицирует сбои по той простой причине, что знает заранее, как должен выглядеть “правильный” спектр. Или, говоря научным языком, он использует априорную информацию о форме спектра, накопленную в процессе работы. Именно на таком сравнении формы спектра с неким стандартом основан следующий этап выявления и коррекции сбоев. Чтобы исключить зависимость формы спектра от величины сигнала, обрабатываемый спектр и стандарт сравниваются в относительных единицах (приводятся к интервалу от 1 до 2), и если модуль их разности превышает СКО стандарта, умноженное на некоторый коэффициент, то спектр идентифицируется как сбойный. Указанный коэффициент подбирается в процессе настройки системы. Конкретно использовался коэффициент 4,2, который отличается от традиционного для статистики интервала в 3 СКО, поскольку в данном случае имеется явная зависимость спектров от уровня атмосферного давления и зенитного угла Солнца, следовательно, и распределение погрешностей результатов измерений далеко от нормального. Для получения стандартов и их СКО предусмотрен двухэтапный режим работы системы. На первом этапе априорная информация отсутствует, и блок сравнения со стандартом выключен. По результатам первого этапа вычисляется стандарт, как среднее арифметическое обработанных спектров, и СКО стандарта (при этом стандарты получаются отдельно для нисходящих потоков и для восходящих над разными типами поверхностей). На втором этапе все спектры обрабатываются вновь, но при включенном блоке сравнения со стандартом. С точки зрения теории систем распознавания образов и селекции указанный алгоритм, накапливающий априорную информацию (опыт работы!), является системой с самообучением. Практика обработки результатов зондировок показывает, что применение систем с самообучением в оперативных алгоритмах предварительного анализа спектрофотометрической информации весьма эффективно. Пример устранения сбоев в спектре приведен на рис.3.4.
Рассмотренные выше этапы обработки результатов измерений связаны с анализом формы спектров. Но, к сожалению, отмечались сбои, при которых спектр имел правильную форму, но недопустимо отличался от “хорошего” спектра по величине сигнала. Для выявления этих ситуаций на следующем этапе работы системы анализировалась зависимость величины потоков от атмосферного давления и зенитного угла Солнца. Эта зависимость нелинейная, но не настолько, чтобы при ее аппроксимации квадратичной функцией возникали слишком большие отклонения отдельных спектров от аппроксимирующей кривой. Если же такие отклонения обнаруживаются, это дает основания проверить соответствующие спектры на наличие сбойных точек. Для каждой длины волны строится аппроксимация зависимости величины потока (отдельно падающего и восходящего) от давления P и косинуса зенитного угла Солнца 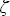 . На примере нисходящего потока его значение определяется по формуле . На примере нисходящего потока его значение определяется по формуле
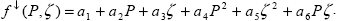 |
(3.2.4) |
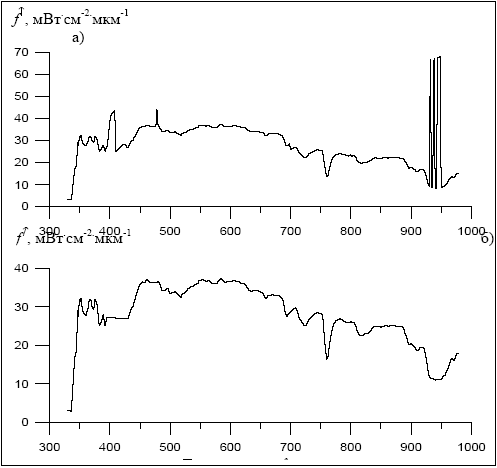
Рисунок 3.4. Пример коррекции спектра по результатам измерений восходящего потока 14.10.1983, время (московское) 7.12, высота 4200 м: а) – исходный спектр; б) – спектр после коррекции
Искомые коэффициенты аппроксимации a1, …, a6 находятся по совокупности измеренных потоков f (Pi,zi) для каждого подъема или спуска зондировки. Система уравнений (3.2.4) решается по МНК, в котором в качестве весов выбираются обратные квадраты случайного СКО потоков (табл.3.1), причем, чтобы потоки, измеренные при больших зенитных углах Солнца, имели меньший вес, в СКО в качестве случайной составляющей погрешности включается и погрешность отклонения от косинусной зависимости. (Pi,zi) для каждого подъема или спуска зондировки. Система уравнений (3.2.4) решается по МНК, в котором в качестве весов выбираются обратные квадраты случайного СКО потоков (табл.3.1), причем, чтобы потоки, измеренные при больших зенитных углах Солнца, имели меньший вес, в СКО в качестве случайной составляющей погрешности включается и погрешность отклонения от косинусной зависимости.
Последний этап системы предварительного анализа зондировок связан с учетом индивидуальных особенностей схемы полета. На этом этапе выбирается (автоматически с последующим “утверждением” оператором) зенитный угол Солнца 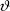 0 ( 0 (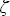 0 =cos 0 =cos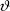 0) и набор атмосферных давлений Pi, i = 1,…,Ni, для которых будут получены окончательные значения потоков как результат вторичной обработки зондировки. Заметим, что для стандартной схемы полета Ni = 6 – значения потоков выдаются для уровней давления от 1000 до 500 мбар с шагом 100 мбар. 0) и набор атмосферных давлений Pi, i = 1,…,Ni, для которых будут получены окончательные значения потоков как результат вторичной обработки зондировки. Заметим, что для стандартной схемы полета Ni = 6 – значения потоков выдаются для уровней давления от 1000 до 500 мбар с шагом 100 мбар.
После проведения описанного предварительного анализа имеем Nj измерений нисходящих потоков f (Pj,zj) и Nk измерений восходящих потоков f (Pj,zj) и Nk измерений восходящих потоков f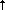 (Pk,zk), из которых требуется получить Ni результатов F (Pk,zk), из которых требуется получить Ni результатов F (Pi,z0) и F (Pi,z0) и F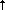 (Pi,z0). Использовавшийся ранее для решения этой задачи алгоритм описан в работе . Однако этот алгоритм основан на применении достаточно многих физически слабо обоснованных допущений, в частности, предположение о линейной зависимости потоков солнечной радиации от зенитного угла Солнца, аппроксимация зависимости потоков от давления полиномом второй степени, предположение о монотонном возрастании восходящего потока с высотой. Поэтому для обработки результатов зондировок, выполненных в 1983 ‑ 1985гг., был разработан новый алгоритм, также основанный на определенных допущениях, но не столь жестких, как в работе . (Pi,z0). Использовавшийся ранее для решения этой задачи алгоритм описан в работе . Однако этот алгоритм основан на применении достаточно многих физически слабо обоснованных допущений, в частности, предположение о линейной зависимости потоков солнечной радиации от зенитного угла Солнца, аппроксимация зависимости потоков от давления полиномом второй степени, предположение о монотонном возрастании восходящего потока с высотой. Поэтому для обработки результатов зондировок, выполненных в 1983 ‑ 1985гг., был разработан новый алгоритм, также основанный на определенных допущениях, но не столь жестких, как в работе .
Запишем зависимость изменения потоков при изменении 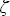 , и P в виде ряда Тейлора, ограничиваясь членами до второго порядка включительно: , и P в виде ряда Тейлора, ограничиваясь членами до второго порядка включительно:
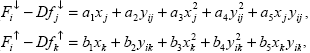 |
(3.2.5) |
где D – поправочный коэффициент, корректирующий систематическую погрешность калибровки, а для краткости введены обозначения Fi  F F (Pi, (Pi,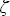 0), Fi 0), Fi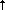  F F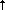 (Pi, (Pi,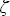 0), fj 0), fj  f f  (Pj, (Pj,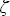 j), fk j), fk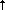  f f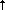 (Pk, (Pk,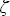 k), xj = k), xj = 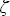 0 - 0 - 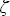 j, xk = j, xk = 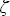 i0 - i0 - 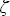 k, yij=Pi -Pj, yik =Pi -Pk. Величинами, подлежащими определению, являются Fi k, yij=Pi -Pj, yik =Pi -Pk. Величинами, подлежащими определению, являются Fi , Fi , Fi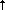 , D, a1,…,a5, b1,…,b5. , D, a1,…,a5, b1,…,b5.
Для решения системы уравнений (3.2.5) следует добавить условия определения калибровочного множителя D. Здесь, так же как в работе [11], необходима экстраполяция значений нисходящего потока на уровень 0 мбар и сравнение их с известным внеатмосферным значением 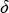 F0 F0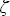 0, где поправка 0, где поправка 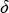 учитывает отклонение расстояния от Земли до Солнца от среднего значения для конкретной даты измерений. Значения F0 заимствованы из работы (рис. 1.3), где приведены современные данные, усредненные по нескольким первоисточникам. Для корректного сравнения внеатмосферных значений потока с измерениями потока прибором К-3, спектральные значения внеатмосферного потока из работы были пересчитаны по формуле (1.1.12) с учетом спектральной аппаратной функции прибора, выраженной формулой (3.1.1). Полученная кривая F0( учитывает отклонение расстояния от Земли до Солнца от среднего значения для конкретной даты измерений. Значения F0 заимствованы из работы (рис. 1.3), где приведены современные данные, усредненные по нескольким первоисточникам. Для корректного сравнения внеатмосферных значений потока с измерениями потока прибором К-3, спектральные значения внеатмосферного потока из работы были пересчитаны по формуле (1.1.12) с учетом спектральной аппаратной функции прибора, выраженной формулой (3.1.1). Полученная кривая F0(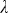 ) приведена на рис.3.5. Значения поправки ) приведена на рис.3.5. Значения поправки 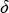 приведены в . В результате для нахождения неизвестных величин и коэффициентов получаем систему линейных уравнений : приведены в . В результате для нахождения неизвестных величин и коэффициентов получаем систему линейных уравнений :
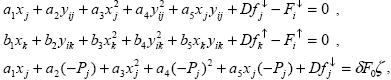 |
(3.2.6) |
Система (3.2.6) состоит из (Nj + Nk)Ni + Nj уравнений относительно 11 + 2Ni неизвестных. Уровни Pi выбирались так, чтобы число уравнений не менее чем вдвое превышало число неизвестных.
Система уравнений (3.2.6) решалась по МНК независимо для каждой длины волны, при этом учитывалась погрешность результатов измерений, т.е. в качестве весов выбирались обратные квадраты случайной СКО (табл. 3.1) с учетом погрешности отклонения от косинусной зависимости (см. выше). Чтобы полученное по МНК формальное математическое решение не противоречило законам физики, необходимо наложить на решение дополнительные условия. Таковыми являются неотрицательность величин лучистых притоков и априорные ограничения на альбедо:
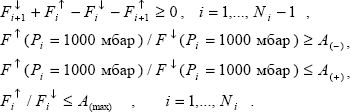 |
(3.2.7) |
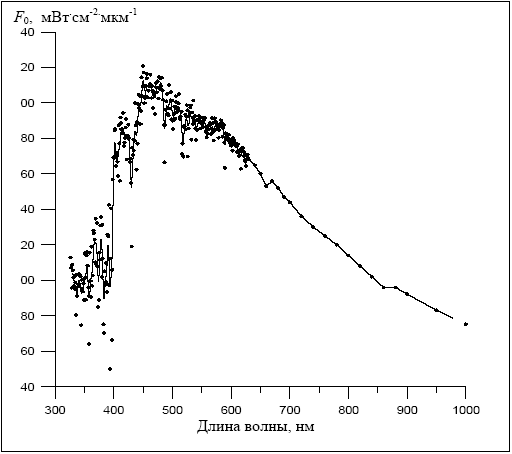
Рисунок 3.5. Спектральная солнечная постоянная с учетом аппаратной функции прибора К-3 (сплошная кривая). Точками показаны исходные значения F0 с высоким спектральным разрешением по [32]
Вторая и третья строки в наборе условий (3.2.7) учитывают априорно известный диапазон спектрального альбедо поверхности: A(-) – минимально возможное значение, A(+) – максимально возможное значение. Конкретные значения A(-) и A(+) выбирались из данных по спектральным отражательным характеристикам тех же поверхностей , , , (коэффициенты спектральной яркости в надире, в приближении ортотропной поверхности равные альбедо, для песка, снега и чистой озерной воды). Эти данные будут рассмотрены в разделе 3.4. Максимальное альбедо системы “атмосфера плюс поверхность” A(max) во всех случаях принималось равным 0,95.
Решение системы уравнений (3.2.6) с учетом связей (3.2.7) осуществлялось итерационным методом. Сначала система уравнений (3.2.6) решалась по МНК без учета выражений (3.2.7) и для полученного решения проверялось выполнение условий (3.2.7). Если все они выполнены – итерации прекращались. Иначе решение по МНК искалось уже с учетом соотношений (3.2.7). При этом учет связей осуществлялся путем перевода неравенств (3.2.7) в строгие равенства и исключения из системы (3.2.6) переменных путем подстановки указанных равенств. Соответствующие формулы, выражающие решения в указанном случае, будут приведены в главе 4. Конкретная схема итераций строилась следующим образом. Сначала исключались Fi+1 из условий для притоков и Fi из условий для притоков и Fi из условий для альбедо. Решение системы (3.2.6) по МНК находилось для каждой исключенной переменной в отдельности (всего 2Ni решений), из них выбиралось то, которому соответствует минимальная невязка. Для этого решения вновь проверялись условия связи (3.2.7). Если они не выполнялись – итерации продолжались, причем далее исключались уже пары условий, потом – тройки и т.д. В наихудшем варианте таким способом требуется перебрать решений, учитывая, что в нашем случае максимальное значение Ni = 6, это приемлемое количество для современных компьютеров. из условий для альбедо. Решение системы (3.2.6) по МНК находилось для каждой исключенной переменной в отдельности (всего 2Ni решений), из них выбиралось то, которому соответствует минимальная невязка. Для этого решения вновь проверялись условия связи (3.2.7). Если они не выполнялись – итерации продолжались, причем далее исключались уже пары условий, потом – тройки и т.д. В наихудшем варианте таким способом требуется перебрать решений, учитывая, что в нашем случае максимальное значение Ni = 6, это приемлемое количество для современных компьютеров.
Окончательным результатом вторичной обработки зондировок являются искомые значения Fi и F и F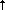 i при i = 1,…,Ni, а также получаемая в МНК ковариационная матрица погрешностей для указанных потоков, причем для дальнейшей интерпретации результатов необходимо сохранять именно всю матрицу, а не только ее диагональ – дисперсии значений потоков. Если решение получено с учетом связей (3.2.7), то часть искомых потоков линейно зависима, следовательно, неинформативна. Индикатор наличия линейной зависимости также записывался в выходные данные вторичной обработки. Подчеркнем, что в силу индивидуального решения системы (3.2.6) с учетом (3.2.7) для каждой длины волны, число независимых, т.е. информативных, потоков в общем случае оказывалось существенно различным для разных длин волн. В качестве дополнительного результата вторичной обработки данных зондировок были коэффициенты D, a1 , …, a5, b1,…, b5 и их СКО. i при i = 1,…,Ni, а также получаемая в МНК ковариационная матрица погрешностей для указанных потоков, причем для дальнейшей интерпретации результатов необходимо сохранять именно всю матрицу, а не только ее диагональ – дисперсии значений потоков. Если решение получено с учетом связей (3.2.7), то часть искомых потоков линейно зависима, следовательно, неинформативна. Индикатор наличия линейной зависимости также записывался в выходные данные вторичной обработки. Подчеркнем, что в силу индивидуального решения системы (3.2.6) с учетом (3.2.7) для каждой длины волны, число независимых, т.е. информативных, потоков в общем случае оказывалось существенно различным для разных длин волн. В качестве дополнительного результата вторичной обработки данных зондировок были коэффициенты D, a1 , …, a5, b1,…, b5 и их СКО.
Укажем три основных источника систематических погрешностей полученных результатов: погрешность значений внеатмосферного потока F0; неадекватность формул (3.2.6) для зависимости значений потока солнечной радиации от давления и косинуса зенитного угла Солнца; изменения параметров атмосферы и поверхности во время измерений. Первая погрешность по оценкам достаточно велика и составляет несколько процентов. Однако, если при интерпретации измерений использовать то же значение F0, что и в формулах (3.2.6), эта погрешность, очевидно, никак не скажется на результатах. Что касается адекватности системы уравнений (3.2.6), то в предыдущей версии алгоритма, предложенной в работе применялись формулы, являющиеся частным случаем (3.2.6) и там же показано, что систематическая погрешность системы уравнений из работы меньше случайной погрешности измерений и может не приниматься во внимание. Тем более этот вывод справедлив для системы более точных уравнений (3.2.6). Наконец, учитывая то обстоятельство, что результаты при решении системы уравнений (3.2.6), исходя из существа метода наименьших квадратов, являются средневзвешенными значениями по всем измеренным спектрам, можно отнести их к неким усредненным по времени и пространству параметрам атмосферы и подстилающей поверхности. Максимальный вклад при этом усреднении дают спектры, полученные во время подробного спуска (просто потому, что в (3.2.6) их много больше, чем остальных спектров). В ходе зондировки подробный спуск длится чуть более часа (см. рис.3.3а), что почти совпадает со временем полета, характерным для радиозондов (около часа). По пространственным масштабам район полетов составлял примерно 30 км, что аналогично характерной горизонтальной длине трассы, пролетаемой радиозондом. Таким образом, можно утверждать, что по степени пространственно-временного усреднения параметров атмосферы полученные данные практически не уступают данным радиозондирования и при этом содержат уникальную информацию о спектральной зависимости радиационных характеристик атмосферы и поверхности. |