Метод Монте-Карло (более “строгое” название – метод статистического моделирования) является, пожалуй, наиболее мощным численным методом теории переноса излучения. Он позволяет решать задачи расчета интенсивности излучения с учетом сферической геометрии, поляризации, неоднородности атмосферы и поверхности и т.д. . Здесь мы будем метод Монте-Карло применять для решения простой, по сравнению с названными, задачи расчета полусферических потоков и интенсивностей солнечного излучения в горизонтально однородной плоскопараллельной атмосфере.
В атмосферной оптике существуют два подхода к изложению метода Монте-Карло в атмосферной оптике , : как метод формального математического решения задач (уравнений) переноса излучения или как метод моделирования физических процессов распространения излучения в атмосфере, когда даже не требуется привлекать собственно аппарат теории переноса. На наш взгляд второй путь проще для понимания, поэтому будем следовать ему, аналогично работе , а затем покажем, что полученный алгоритм согласуется с математической постановкой задачи, изложенной в разделе 1.3.
В отличие от других методов, в методе Монте-Карло удобно не разделять прямое, рассеянное и отраженное от поверхности излучение. Так же, по причинам, которые выяснятся в гл. 5, мы будем рассматривать в качестве вертикальной координаты не оптическую глубину  , а высоту z. , а высоту z.
Таким образом, будем решать задачу, для которой модель атмосферы показана на рис. 2.1. Пусть имеется плоскопараллельная горизонтально однородная атмосфера, на верхнюю границу z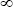 которой падает параллельный поток солнечного излучения направления ( которой падает параллельный поток солнечного излучения направления (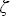 ,0) и величиной потока на перпендикулярную направлению падения площадку F0 = ,0) и величиной потока на перпендикулярную направлению падения площадку F0 = 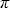 S. Нижней границей атмосферы z = 0 является ортотропная поверхность с альбедо A (заметим, что требование ортотропности отражения не является существенным для метода Монте-Карло, мы рассмотрим модель анизотропного отражения в гл.5). Оптические параметры атмосферы задаются в виде таблиц по высотной сетке: объемный коэффициент ослабления как S. Нижней границей атмосферы z = 0 является ортотропная поверхность с альбедо A (заметим, что требование ортотропности отражения не является существенным для метода Монте-Карло, мы рассмотрим модель анизотропного отражения в гл.5). Оптические параметры атмосферы задаются в виде таблиц по высотной сетке: объемный коэффициент ослабления как  (zi), вероятность выживания кванта как (zi), вероятность выживания кванта как  0(zi), индикатриса рассеяния еще и как таблица по косинусам углов рассеяния x(zi, 0(zi), индикатриса рассеяния еще и как таблица по косинусам углов рассеяния x(zi,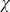 j), j = 1,…,M, j), j = 1,…,M, 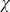 1 = 1, 1 = 1, 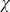 M = -1, где i = 1,…,N, z1 = z M = -1, где i = 1,…,N, z1 = z , zN =0. Заметим, что все указанные параметры, в свою очередь, определяются физической моделью атмосферы – вертикальными профилями температуры, давления, концентраций поглощающих излучения газов и аэрозольной моделью – см. раздел 1.2. Требуется (численно) найти полусферические потоки: нисходящий F , zN =0. Заметим, что все указанные параметры, в свою очередь, определяются физической моделью атмосферы – вертикальными профилями температуры, давления, концентраций поглощающих излучения газов и аэрозольной моделью – см. раздел 1.2. Требуется (численно) найти полусферические потоки: нисходящий F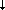 (z), восходящий F (z), восходящий F (z) на произвольной высоте 0 (z) на произвольной высоте 0 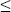 z z  z z или (и) интенсивность рассеянного излучения I(z, или (и) интенсивность рассеянного излучения I(z, , , ) для произвольного направления ( ) для произвольного направления ( , , ). Все указанные параметры и величины являются монохроматическими для заданной длины волны. ). Все указанные параметры и величины являются монохроматическими для заданной длины волны.
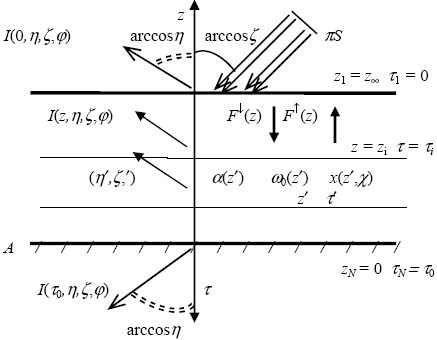
Рисунок 2.1. Модель атмосферы
Прежде чем излагать собственно метод Монте-Карло, найдем по (1.3.8) оптическую глубину атмосферы как функцию высоты. Применяя квадратурную формулу трапеций, получаем
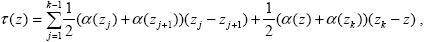 |
(2.1.1) |
где номер k определяется из условия zk+1< z 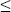 zk. Введем естественно возникающую из (2.1.1) таблицу оптических глубин zk. Введем естественно возникающую из (2.1.1) таблицу оптических глубин
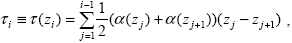 |
(2.1.2) |
где i = 1,…,N, причем  1=0, 1=0,  N = N =  0 – оптическая толщина атмосферы (1.3.9). Договоримся здесь и далее, в соответствии с квадратурной формулой трапеций, для сетки высот использовать линейную интерполяцию. Тогда в выражении (2.1.1) 0 – оптическая толщина атмосферы (1.3.9). Договоримся здесь и далее, в соответствии с квадратурной формулой трапеций, для сетки высот использовать линейную интерполяцию. Тогда в выражении (2.1.1)
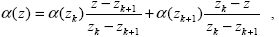 |
(2.1.3) |
что с учетом (2.1.2) дает полином второй степени
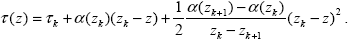 |
(2.1.4) |
Определив функцию  (z) по (2.1.2), (2.1.4) мы можем использовать в качестве координаты оптическую глубину, как это предписывает теория переноса и как удобно на практике. При этом исходные таблицы оптических параметров атмосферы согласно (2.1.2) непосредственно переходят в (z) по (2.1.2), (2.1.4) мы можем использовать в качестве координаты оптическую глубину, как это предписывает теория переноса и как удобно на практике. При этом исходные таблицы оптических параметров атмосферы согласно (2.1.2) непосредственно переходят в  ( ( i), i),  0( 0( i) и x( i) и x( i, i, i), i = 1,…,N, а для поиска промежуточных значений, например i), i = 1,…,N, а для поиска промежуточных значений, например  0( 0( ), можно либо использовать линейную интерполяцию (2.1.3) непосредственно по ), можно либо использовать линейную интерполяцию (2.1.3) непосредственно по  , либо, что более корректно, находить высоту как z( , либо, что более корректно, находить высоту как z( ) и интерполировать в формуле (2.1.3) по высоте. При этом из соотношения (2.1.4) обратная функция z( ) и интерполировать в формуле (2.1.3) по высоте. При этом из соотношения (2.1.4) обратная функция z( ) получается как ) получается как
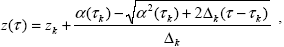 |
(2.1.5) |
где номер k находится из условия  k k 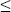  < <  k+1, а k+1, а 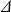 k = [ k = [ ( ( k) – k) –  ( ( k+1)] / [zk – zk+1]. Заметим, что, поскольку этот прием согласования осей высоты и оптической глубины никак не связан с особенностями метода Монте-Карло, его, вероятно, можно успешно использовать и в других численных методах теории переноса излучения. k+1)] / [zk – zk+1]. Заметим, что, поскольку этот прием согласования осей высоты и оптической глубины никак не связан с особенностями метода Монте-Карло, его, вероятно, можно успешно использовать и в других численных методах теории переноса излучения.
Перейдем, наконец, к непосредственному изложению метода Монте-Карло. Метод Монте-Карло основан на представлении переноса излучения в атмосфере в виде случайного процесса: движения через среду условных частиц света, называемых “фотонами”, моделирования реализаций этого процесса на ЭВМ и вычисления требуемых характеристик как математического ожидания случайных величин, возникающих при этих реализациях , .
Для статистического моделирования на компьютере необходимо воспроизвести некоторый процесс, который будет играть роль “слепого случая”. Подобные алгоритмы, называемые “генераторы случайных чисел”, в настоящее время хорошо известны и мы не будем останавливаться на их особенностях, указав лишь, что конкретно использовали генератор, предложенный в работе , . В основу метода Монте-Карло положена совокупность случайных чисел, равномерно распределенных на интервале [0,1]. Договоримся в дальнейшем под термином “случайное число” понимать только такие числа, обозначать их буквой 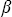 и при каждом ее появлении в тексте подразумевать новое случайное число. Для компактной записи возникающих в методе Монте-Карло многочисленных рекуррентных соотношений договоримся использовать, как принято в языках программирования, операцию присваивания “:=”. (Для читателей, не владеющих программированием, поясним, что она означает присваивание переменной слева от знака “:=” численного значения выражения, стоящего справа; например, b:=b + 10, есть “значение переменной b на текущей итерации равно значению b на предыдущей итерации плюс 10”). и при каждом ее появлении в тексте подразумевать новое случайное число. Для компактной записи возникающих в методе Монте-Карло многочисленных рекуррентных соотношений договоримся использовать, как принято в языках программирования, операцию присваивания “:=”. (Для читателей, не владеющих программированием, поясним, что она означает присваивание переменной слева от знака “:=” численного значения выражения, стоящего справа; например, b:=b + 10, есть “значение переменной b на текущей итерации равно значению b на предыдущей итерации плюс 10”).
Пусть вероятность некоторого дискретного случайного события равна P. Тогда выберем случайное число и если 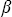 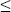 P, то будем считать (при моделировании), что событие произошло, в противном случае – не произошло. Обоснование такого приема очевидно: если устремить число актов моделирования к бесконечности, то, в силу равномерного распределения случайных чисел, мы найдем, что отношение числа актов моделирования, когда событие произошло, к числу всех актов, т.е. вероятность события, как раз и равно P. Для моделирования непрерывной случайной величины, характеризующейся на интервале [a,b] плотностью вероятности P, то будем считать (при моделировании), что событие произошло, в противном случае – не произошло. Обоснование такого приема очевидно: если устремить число актов моделирования к бесконечности, то, в силу равномерного распределения случайных чисел, мы найдем, что отношение числа актов моделирования, когда событие произошло, к числу всех актов, т.е. вероятность события, как раз и равно P. Для моделирования непрерывной случайной величины, характеризующейся на интервале [a,b] плотностью вероятности 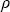 (u), достаточно заметить, что, по определению, вероятность появления значения u из интервала [a,u] равна (u), достаточно заметить, что, по определению, вероятность появления значения u из интервала [a,u] равна 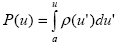 , что при применении описанного выше метода для дискретных случайных величин непосредственно приводит для моделирования значений u к уравнению , что при применении описанного выше метода для дискретных случайных величин непосредственно приводит для моделирования значений u к уравнению
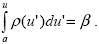 |
(2.1.6) |
Как отмечено выше, процесс переноса излучения в методе Монте-Карло моделируется как движение фотонов. Фотон, попадая в атмосферу, описывает в ней некоторую траекторию, которая заканчивается либо его вылетом из атмосферы, либо поглощением в атмосфере или на подстилающей поверхности. Положение фотона в атмосфере полностью определяется тремя координатами:  ', ',  ', ',  ', следовательно, моделирование траектории фотона сводится к последовательному пересчету данных координат. А для этого достаточно уметь моделировать всего три процесса: свободный (т.е. без взаимодействия с атмосферой) пробег фотона, взаимодействие фотона с атмосферой (поглощение и рассеяние), взаимодействие фотона с поверхностью (поглощение и отражение). ', следовательно, моделирование траектории фотона сводится к последовательному пересчету данных координат. А для этого достаточно уметь моделировать всего три процесса: свободный (т.е. без взаимодействия с атмосферой) пробег фотона, взаимодействие фотона с атмосферой (поглощение и рассеяние), взаимодействие фотона с поверхностью (поглощение и отражение).
Свободный пробег фотона аналогичен прохождению через атмосферу прямого излучения Солнца. Рассмотрим формулу закона Бугера для потока прямого излучения (1.3.11): Fd( ) = F0 ) = F0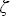 e- e- / /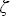 . Пусть на верхнюю границу атмосферы падают K фотонов, т.е. F0 . Пусть на верхнюю границу атмосферы падают K фотонов, т.е. F0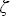 = KE, где E – энергия одного фотона. Подставляя KE в закон Бугера, получаем, что число фотонов, дошедших до оптической глубины = KE, где E – энергия одного фотона. Подставляя KE в закон Бугера, получаем, что число фотонов, дошедших до оптической глубины  есть K( есть K( )=Ke- )=Ke- / /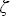 . Но ведь, согласно определению вероятности, это означает, что вероятность достижения фотоном глубины . Но ведь, согласно определению вероятности, это означает, что вероятность достижения фотоном глубины  есть e- есть e- / /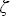 . Заменяя z на произвольное направление . Заменяя z на произвольное направление  ' и обозначая длину свободного пробега как ' и обозначая длину свободного пробега как 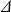  ' из метода моделирования непрерывных случайных величин получаем ' из метода моделирования непрерывных случайных величин получаем
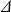  ' = - ' = - ' ln ' ln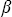 , ,  ' := ' :=  '+ '+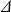  ' . ' . |
(2.1.7) |
Заметим, что, во-первых, соотношения (2.1.7) справедливы как при движении фотона вниз ( ' >0 и ' >0 и  ' увеличивается), так и при движении вверх ( ' увеличивается), так и при движении вверх ( ' < 0 и ' < 0 и  ' уменьшается). Во-вторых, при выводе соотношений (2.1.7) мы обошлись без получения явного вида функции плотности вероятности свободного пробега фотона, однако далее она нам понадобится. Так как из вышеизложенного следует, что вероятность пробега от 0 до ' уменьшается). Во-вторых, при выводе соотношений (2.1.7) мы обошлись без получения явного вида функции плотности вероятности свободного пробега фотона, однако далее она нам понадобится. Так как из вышеизложенного следует, что вероятность пробега от 0 до  есть P( есть P( ) = 1 ‑ e- ) = 1 ‑ e- / /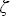 , дифференцируя по , дифференцируя по  , получаем , получаем
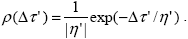 |
(2.1.8) |
Вероятность рассеяния фотона в атмосфере есть (непосредственно по терминологии – вероятность выживания кванта!)  0( 0( '). Таким образом, если '). Таким образом, если 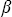 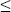  0( 0( '), то происходит рассеяние фотона, в противном случае – поглощение его в атмосфере, что означает конец траектории. В случае рассеяния требуется определить косинус угла рассеяния '), то происходит рассеяние фотона, в противном случае – поглощение его в атмосфере, что означает конец траектории. В случае рассеяния требуется определить косинус угла рассеяния 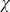 и азимут рассеяния и азимут рассеяния 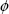 . Поскольку индикатриса рассеяния от азимута не зависит, то он распределен равномерно на интервале [0,2 . Поскольку индикатриса рассеяния от азимута не зависит, то он распределен равномерно на интервале [0,2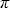 ], что дает ], что дает 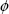 =2 =2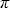 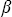 . Плотность вероятности рассеяния на угол с косинусом . Плотность вероятности рассеяния на угол с косинусом 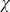 есть (опять же по определению (1.1.2) из раздела 1.1!) индикатриса рассеяния x( есть (опять же по определению (1.1.2) из раздела 1.1!) индикатриса рассеяния x(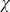 ). В силу ее табличного задания, исходя из правила моделирования (2.1.6), повторяя дословно рассуждения при выводе формул (2.1.1) ‑ (2.1.5) и учитывая множитель 1/2 в нормировочном соотношении (1.2.7), получаем ). В силу ее табличного задания, исходя из правила моделирования (2.1.6), повторяя дословно рассуждения при выводе формул (2.1.1) ‑ (2.1.5) и учитывая множитель 1/2 в нормировочном соотношении (1.2.7), получаем
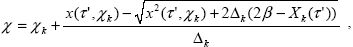 |
(2.1.9) |
где
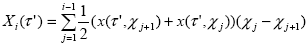 ,, ,,
номер k определяется из условия 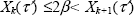 (здесь значение (здесь значение 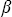 то же, что в (2.1.9)), а то же, что в (2.1.9)), а
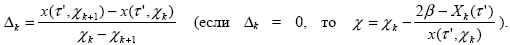
Заметим, что в силу линейной связи Xj( ') и x( ') и x( ', ',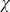 j), удобно предварительно по исходным индикатрисам получать таблицу Xj(zi), j = 1,…,M, i = 1,…,N и использовать ее для интерполяционного вычисления Xj( j), удобно предварительно по исходным индикатрисам получать таблицу Xj(zi), j = 1,…,M, i = 1,…,N и использовать ее для интерполяционного вычисления Xj( ') по формулам (2.1.3), (2.1.5). После рассеяния фотона требуется определить новое направление его движения. Эта несложная задача сводится к решению сферических треугольников [5]. Обозначая направление фотона до рассеяния величиной ') по формулам (2.1.3), (2.1.5). После рассеяния фотона требуется определить новое направление его движения. Эта несложная задача сводится к решению сферических треугольников [5]. Обозначая направление фотона до рассеяния величиной  1' = 1' =  ', имеем : ', имеем :
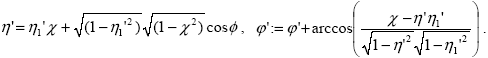 |
(2.1.10) |
При взаимодействии излучения с подстилающей поверхностью, альбедо также можно приписать очевидный смысл вероятности отражения. Тогда если 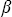 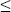 A, то происходит отражение, в противном случае – поглощение фотона на поверхности и конец его траектории. В силу ортотропности отражения, все возможные направления фотона после отражения распределены равномерно, поэтому A, то происходит отражение, в противном случае – поглощение фотона на поверхности и конец его траектории. В силу ортотропности отражения, все возможные направления фотона после отражения распределены равномерно, поэтому
 '=-cos( '=-cos(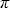 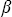 /2), /2),  ' = 2 ' = 2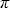 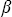 , ,  ' = ' =  0 . 0 . |
(2.1.11) |
Теперь, для вычисления искомых потоков, повторив приведенные выше рассуждения при получении длины свободного пробега, находим, что достаточно подсчитать число фотонов, проходящих уровень  (z) в нужном направлении, т.е. вниз ( (z) в нужном направлении, т.е. вниз ( ' > 0) для F ' > 0) для F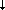 (z) и вверх ( (z) и вверх ( ' < 0) для F ' < 0) для F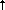 (z). Введем для этого величины x1 (z). Введем для этого величины x1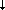 (z) и x2 (z) и x2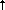 (z) с нулевыми начальными значениями. Пусть (z) с нулевыми начальными значениями. Пусть  '1 – координата фотона до моделирования свободного пробега (2.1.7), а '1 – координата фотона до моделирования свободного пробега (2.1.7), а  '2 = '2 =  '1 + D '1 + D ' – после моделирования. Тогда : ' – после моделирования. Тогда :
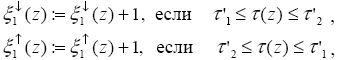 |
(2.1.12) |
(при этом выражения (2.1.12) применяются также и в случае, если фотон вылетел из атмосферы ( '2 < 0) или достиг поверхности ( '2 < 0) или достиг поверхности ( '2 '2   0)). После моделирования некоторого числа K траекторий, искомые потоки находятся как число “сосчитанных” фотонов, умноженное на энергию одного фотона, которая (см. выше) равна F0 0)). После моделирования некоторого числа K траекторий, искомые потоки находятся как число “сосчитанных” фотонов, умноженное на энергию одного фотона, которая (см. выше) равна F0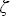 /K. Таким образом, получаем : /K. Таким образом, получаем :
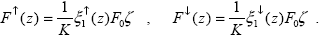 |
(2.1.13) |
Договоримся далее величины типа x1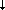 (z) и x1 (z) и x1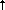 (z) именовать “счетчики”, а выражения вида (2.1.12) – “запись в счетчики”. (z) именовать “счетчики”, а выражения вида (2.1.12) – “запись в счетчики”.
Может показаться, что выражения (2.1.12) противоречат формуле связи величин потока и интенсивности (1.1.4), т.к. не учитывают косинус зенитного угла фотона. Однако фотон является “переносчиком” именно потока излучения, а не интенсивности. Это легко понять физически: если в качестве фотона мы возьмем реальный квант света, то его энергия, очевидно, не зависит от направления движения. Формальное же доказательство справедливости выражений (2.1.12) элементарно. Рассмотрим траекторию единственного фотона (K=1). Пусть, претерпев однократное рассеяние в атмосфере, фотон вылетает через ее верхнюю границу. Тогда по закону сохранения энергии величина восходящего потока на верхней границе (2.1.13) должна быть равна величине нисходящего потока (актов поглощения не было), а это условие не будет нарушено, только в том случае, если запись в счетчики по формуле (2.1.12) не зависит от величины  '. '.
Резюмируя, получаем следующий алгоритм расчета потоков. В начале каждой траектории имеем  ' = 0, ' = 0,  ' = ' = 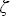 , ,  ' =0. Далее моделируем свободный пробег фотона по формуле (2.1.7) с записью в счетчики (2.1.12). Если фотон вылетел из атмосферы ( ' =0. Далее моделируем свободный пробег фотона по формуле (2.1.7) с записью в счетчики (2.1.12). Если фотон вылетел из атмосферы ( ' ' 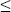 0) – конец его траектории – осуществляется переход на моделирование траектории следующего фотона. Если фотон достиг подстилающей поверхности ( 0) – конец его траектории – осуществляется переход на моделирование траектории следующего фотона. Если фотон достиг подстилающей поверхности ( ' '   0), то моделируем взаимодействие (поглощение или отражение) с поверхностью, в случае поглощения – конец траектории, в случае отражения – получаем новое направление по (2.1.11) и переходим к моделированию очередного свободного пробега. Если фотон остался в атмосфере (0T0), то моделируем его взаимодействие (поглощение или рассеяние) с атмосферой, в случае поглощения – конец траектории, в случае рассеяния определяем новое направление по (2.1.9), (2.1.10) и переходим к моделированию следующего свободного пробега фотона. После рассмотрения достаточно большого числа K траекторий, искомые величины потоков находим по формулам (2.1.13). 0), то моделируем взаимодействие (поглощение или отражение) с поверхностью, в случае поглощения – конец траектории, в случае отражения – получаем новое направление по (2.1.11) и переходим к моделированию очередного свободного пробега. Если фотон остался в атмосфере (0T0), то моделируем его взаимодействие (поглощение или рассеяние) с атмосферой, в случае поглощения – конец траектории, в случае рассеяния определяем новое направление по (2.1.9), (2.1.10) и переходим к моделированию следующего свободного пробега фотона. После рассмотрения достаточно большого числа K траекторий, искомые величины потоков находим по формулам (2.1.13).
Заметим, что отношения  1 1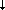 (z)/K и (z)/K и  1 1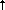 (z)/K, согласно (2.1.11), есть ни что иное, как математические ожидания (средние арифметические) числа фотонов, записанных в счетчики в результате моделирования одной траектории фотона. Введем счетчики (z)/K, согласно (2.1.11), есть ни что иное, как математические ожидания (средние арифметические) числа фотонов, записанных в счетчики в результате моделирования одной траектории фотона. Введем счетчики  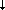 (z) и (z) и   (z) с нулевыми значениями в начале каждой траектории и соотношениями записи аналогичными (2.1.12), но уже опять-таки для одной траектории. Тогда выражения (2.1.12) перепишутся как (z) с нулевыми значениями в начале каждой траектории и соотношениями записи аналогичными (2.1.12), но уже опять-таки для одной траектории. Тогда выражения (2.1.12) перепишутся как
 |
(2.1.14) |
причем в формулах (2.1.14) запись в счетчики  1 1 (z) и (z) и  1 1 (z) осуществляется в конце каждой траектории фотона. (z) осуществляется в конце каждой траектории фотона.
Таким образом, задача расчета потоков методом Монте-Карло по сути сводится к вычислению по конечной выборке из K траекторий (2.1.13), (2.1.14) математического ожидания случайных величин   (z) и (z) и   (z) – числа фотонов, попадающих в счетчик за одну траекторию. Но ведь помимо математического ожидания несложно вычислять и другие статистические оценки случайных величин (z) – числа фотонов, попадающих в счетчик за одну траекторию. Но ведь помимо математического ожидания несложно вычислять и другие статистические оценки случайных величин  (z) и (z) и   (z). Найдем их дисперсию. Введем счетчики квадратов (z). Найдем их дисперсию. Введем счетчики квадратов  2 2 (z) и (z) и  2 2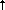 (z) с нулевыми начальными значениями и одновременно с (2.1.14) будем записывать (z) с нулевыми начальными значениями и одновременно с (2.1.14) будем записывать
 |
(2.1.15) |
Используя известное выражение для дисперсии D( ) = M( ) = M( 2) – M2( 2) – M2( ), где M(…) – математическое ожидание, получаем ), где M(…) – математическое ожидание, получаем
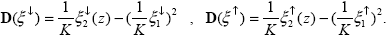 |
(2.1.16) |
Закон распределения самих случайных величин  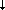 (z) и (z) и  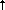 (z) неизвестен. Однако распределение их математических ожиданий, согласно центральной предельной теореме, стремится к нормальному при K -> (z) неизвестен. Однако распределение их математических ожиданий, согласно центральной предельной теореме, стремится к нормальному при K ->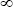 . Следовательно, искомые потоки излучения (2.1.13), которые естественно тоже рассматривать как случайные величины, имеют распределения, асимптотически близкие к нормальному. Нормальное распределение, как известно, характеризуется математическим ожиданием и дисперсией, но здесь уже применительно не к величинам . Следовательно, искомые потоки излучения (2.1.13), которые естественно тоже рассматривать как случайные величины, имеют распределения, асимптотически близкие к нормальному. Нормальное распределение, как известно, характеризуется математическим ожиданием и дисперсией, но здесь уже применительно не к величинам  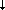 (z) и (z) и  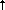 (z), а к самим потокам, каждый из которых есть случайная величина с дисперсией выражаемой формулами (2.1.16). Это, учитывая известное правило сложения дисперсии, дает согласно работе [2] (см. также раздел 4.3) для среднеквадратического отклонения (СКО) (s(…)=(D(…))1/2) потоков (z), а к самим потокам, каждый из которых есть случайная величина с дисперсией выражаемой формулами (2.1.16). Это, учитывая известное правило сложения дисперсии, дает согласно работе [2] (см. также раздел 4.3) для среднеквадратического отклонения (СКО) (s(…)=(D(…))1/2) потоков
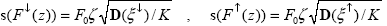 |
(2.1.17) |
Из формул (2.1.17) следует, что чем больше число траекторий K, тем меньше СКО, т.е. случайная погрешность вычислений потоков излучения. Оценка СКО по соотношениям (2.1.15)‑(2.1.17) имеет важное практическое значение, поскольку позволяет проводить расчеты с заранее заданной точностью. Действительно, вычисляя СКО величин потоков излучения можно оценить необходимое количество прослеженных траекторий фотонов: как только значение СКО становится меньше заданного, процесс моделирования прекращают.
Рассмотренная выше схема моделирования траекторий фотонов и вычисления потоков носит название “прямого моделирования” , поскольку она непосредственно отражает наши представления о движении фотонов в атмосфере. Но для ускорения счета по алгоритмам метода Монте-Карло, а также для вычисления величин интенсивностей излучения, прямого моделирования оказывается недостаточно . Рассмотрим два приема повышения эффективности вычислений, которые были использованы в наших расчетах. Подробное описание других методов можно найти в работах , .
Основой для оптимизации расчетов по методу Монте-Карло является идея уменьшения разброса значений, записываемых в счетчики. В этом случае уменьшается величина дисперсии, выражающаяся формулами (2.1.16) и для достижения заданной точности согласно выражению (2.1.17) требуется меньше траекторий.
Допустим, что фотон может делиться на части (здесь это ведь не реальный квант света, а математический объект). Тогда при каждом взаимодействии с атмосферой часть фотона, равная 1 -  0( 0( ') поглощается, а оставшаяся часть ') поглощается, а оставшаяся часть  0( 0( ') рассеивается и продолжает “полет”. При взаимодействии с поверхностью эти части будут, соответственно, равны 1-A и A (A – альбедо подстилающей поверхности). Введем специальную величину w', называемую весом фотона , (которую формально можно рассматривать как четвертую координату), положим w' = 1 в начале каждой траектории и при записи в счетчики (2.1.12) вместо единицы будем прибавлять w'. Тогда, очевидно, моделирование взаимодействия с атмосферой сведется к присвоению на каждом шаге: w':=w' ') рассеивается и продолжает “полет”. При взаимодействии с поверхностью эти части будут, соответственно, равны 1-A и A (A – альбедо подстилающей поверхности). Введем специальную величину w', называемую весом фотона , (которую формально можно рассматривать как четвертую координату), положим w' = 1 в начале каждой траектории и при записи в счетчики (2.1.12) вместо единицы будем прибавлять w'. Тогда, очевидно, моделирование взаимодействия с атмосферой сведется к присвоению на каждом шаге: w':=w' 0( 0( '), а взаимодействия с поверхностью – к присвоению: w':= w'A. Теперь траектория фотона при этих процессах оборваться не может (всегда останется “выжившая” часть фотона), обрыв происходит лишь при вылете из атмосферы через верхнюю границу. Обычно, чтобы не “гонять” по атмосфере фотоны со слишком малым весом, вводят параметр обрыва траектории W: траектория обрывается, при условии w'<W. Значение величины W удобно оценивать исходя из требуемой точности вычислений: W=s '), а взаимодействия с поверхностью – к присвоению: w':= w'A. Теперь траектория фотона при этих процессах оборваться не может (всегда останется “выжившая” часть фотона), обрыв происходит лишь при вылете из атмосферы через верхнюю границу. Обычно, чтобы не “гонять” по атмосфере фотоны со слишком малым весом, вводят параметр обрыва траектории W: траектория обрывается, при условии w'<W. Значение величины W удобно оценивать исходя из требуемой точности вычислений: W=s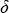 , где s – минимальная (по всем z для падающих и восходящих потоков) требуемая относительная погрешность вычислений, , где s – минимальная (по всем z для падающих и восходящих потоков) требуемая относительная погрешность вычислений, 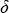 – малое число (конкретно использовалось – малое число (конкретно использовалось 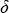 =10-2). Описанный прием “деления” фотона известен под очень неудачным названием “аналитическое усреднение поглощения” (выражение “аналитическое усреднение” ассоциируется с неким приближением, чего в данном случае, конечно же, нет). =10-2). Описанный прием “деления” фотона известен под очень неудачным названием “аналитическое усреднение поглощения” (выражение “аналитическое усреднение” ассоциируется с неким приближением, чего в данном случае, конечно же, нет).
Рассмотрим фотон в начале траектории на верхней границе атмосферы. В этом случае, еще до моделирования его первого свободного пробега (когда  '=0, '=0,  ' = ' = 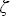 , ,  ' =1), мы, пользуясь законом Бугера (1.3.11), можем отдельно учесть прямое излучение, т.е. доходящее до уровня ' =1), мы, пользуясь законом Бугера (1.3.11), можем отдельно учесть прямое излучение, т.е. доходящее до уровня  (z) без учета взаимодействия с атмосферой, записав в (2.1.12) во все счетчики (z) без учета взаимодействия с атмосферой, записав в (2.1.12) во все счетчики  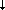 (z) вместо единицы, зависящие от z величины (z) вместо единицы, зависящие от z величины
 |
(2.1.18) |
а далее, при моделировании первого свободного пробега (прямого излучения), запись в счетчики уже не производить. Но указанный прием легко распространить и на дальнейшие отрезки траектории: перед моделированием свободного пробега фотона в счетчики, до которых может долететь фотон (  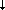 (z), если (z), если  '>0 и '>0 и  ≥ ≥  ', или ', или  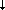 (z), если (z), если  '<0 и '<0 и  ≤ ≤  ′), записывается, величина ′), записывается, величина 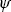 , вычисляемая по формуле (2.1.18), запись же при “пролете” фотоном счетчика уже не производится. Заметим, что экспонента в формуле (2.1.18) есть, как показано выше, вероятность достижения фотоном, “стартующим” с уровня , вычисляемая по формуле (2.1.18), запись же при “пролете” фотоном счетчика уже не производится. Заметим, что экспонента в формуле (2.1.18) есть, как показано выше, вероятность достижения фотоном, “стартующим” с уровня  ', оптической глубины ', оптической глубины  . Этот общий прием, состоящий в записи в счетчик вероятности попадания в него фотона, называется “простой локальной оценкой” , . . Этот общий прием, состоящий в записи в счетчик вероятности попадания в него фотона, называется “простой локальной оценкой” , .
Анализ описанного выше алгоритма расчета полусферических потоков показывает, что на самом деле они не зависят от азимута фотона  '. Действительно, вычисляемый только в двух случаях (2.1.10) и (2.1.11) азимут '. Действительно, вычисляемый только в двух случаях (2.1.10) и (2.1.11) азимут  ' никак не влияет на остальные координаты и, следовательно, на записываемые в счетчики величины. Таким образом, координата “азимут фотона” в данной задаче является излишней и для ускорения вычислений ее можно вообще не вводить (но только именно в данной задаче расчета величин потоков излучения над ортотропной поверхностью). ' никак не влияет на остальные координаты и, следовательно, на записываемые в счетчики величины. Таким образом, координата “азимут фотона” в данной задаче является излишней и для ускорения вычислений ее можно вообще не вводить (но только именно в данной задаче расчета величин потоков излучения над ортотропной поверхностью).
Рассмотрим теперь вторую, из сформулированных ранее, задачу расчета интенсивности излучения I(z, , , ). Очевидно, что процедуры моделирования траекторий фотонов и вычисления математического ожидания и дисперсии не зависят от конкретной вычисляемой величины, следовательно, они не претерпят изменений. Отличие будет лишь в процедуре записи в счетчики величин. Опишем вокруг направления ( ). Очевидно, что процедуры моделирования траекторий фотонов и вычисления математического ожидания и дисперсии не зависят от конкретной вычисляемой величины, следовательно, они не претерпят изменений. Отличие будет лишь в процедуре записи в счетчики величин. Опишем вокруг направления ( , , ) конус с малым телесным углом ) конус с малым телесным углом 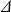 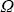 ( ( , , ), и будем записывать в счетчик для интенсивности I все фотоны, пролетающие уровень z и попадающие в данный конус по формуле, аналогичной (2.1.12). Причем, если для потоков в (2.1.12) мы записывали в счетчики единицу, то для интенсивностей, чтобы удовлетворить формуле связи потока и интенсивности (1.1.4), мы, вместо единицы, должны записывать величину 1/| ), и будем записывать в счетчик для интенсивности I все фотоны, пролетающие уровень z и попадающие в данный конус по формуле, аналогичной (2.1.12). Причем, если для потоков в (2.1.12) мы записывали в счетчики единицу, то для интенсивностей, чтобы удовлетворить формуле связи потока и интенсивности (1.1.4), мы, вместо единицы, должны записывать величину 1/| |. Перейдем далее от описанной выше (но не реализуемой на практике) схемы прямого моделирования интенсивностей к схемам весового моделирования и простой локальной оценки. Пусть фотон имеет координаты ( |. Перейдем далее от описанной выше (но не реализуемой на практике) схемы прямого моделирования интенсивностей к схемам весового моделирования и простой локальной оценки. Пусть фотон имеет координаты ( ', ', ', ', '). По определению индикатрисы, как плотности вероятности рассеяния (см. раздел 1.2) вероятность попадания фотона после акта рассеяния на уровне '). По определению индикатрисы, как плотности вероятности рассеяния (см. раздел 1.2) вероятность попадания фотона после акта рассеяния на уровне  ' в телесный угол ' в телесный угол 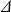 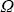 ( ( , , ) равна интегралу от индикатрисы в интервале углов, определяемым ) равна интегралу от индикатрисы в интервале углов, определяемым 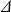 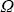 и “нужным” углом рассеяния и “нужным” углом рассеяния 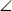 ( ( ', ', ')( ')( ,j), с учетом нормировочного множителя 1/4 ,j), с учетом нормировочного множителя 1/4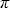 (1.2.6). Устремляя (1.2.6). Устремляя 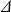 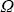 к нулю, находим, что, согласно определению плотности вероятности, вероятность попадания фотона в «нужное» направление ( к нулю, находим, что, согласно определению плотности вероятности, вероятность попадания фотона в «нужное» направление ( , , ) есть просто значение индикатрисы для аргумента ) есть просто значение индикатрисы для аргумента 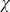 '=cos( '=cos(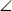 ( ( ', ', ')( ')( , , )), которое вычисляется по формуле (1.3.15). Эту вероятность следует еще умножить на (2.1.18) – вероятность достижения фотоном уровня )), которое вычисляется по формуле (1.3.15). Эту вероятность следует еще умножить на (2.1.18) – вероятность достижения фотоном уровня  (z). Окончательно получаем следующую простую локальную оценку для интенсивности излучения согласно результатам работ , (z). Окончательно получаем следующую простую локальную оценку для интенсивности излучения согласно результатам работ ,
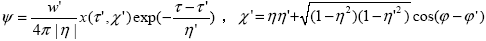 |
(2.1.19) |
Таким образом, рассмотренный алгоритм расчета интенсивностей излучения по методу Монте-Карло отличается от приведенного выше алгоритма расчета потоков только другой формулой для величины простой локальной оценки (2.1.19) вместо (2.1.18) и, соответственно, другими формулами для счетчиков: интенсивности за траекторию  (z, (z, , , ), математического ожидания ), математического ожидания  1(z, 1(z, , , ) и квадрата математического ожидания ) и квадрата математического ожидания  2(z, 2(z, , , ). Оба алгоритма (для интенсивности и для потока излучения) могут быть реализованы на компьютере в едином вычислительном коде. Отметим также, что мы никак не использовали условия безоблачности атмосферы (т.е. ее малой оптической толщины), поэтому алгоритмы метода Монте-Карло могут применяться и для облачного случая. ). Оба алгоритма (для интенсивности и для потока излучения) могут быть реализованы на компьютере в едином вычислительном коде. Отметим также, что мы никак не использовали условия безоблачности атмосферы (т.е. ее малой оптической толщины), поэтому алгоритмы метода Монте-Карло могут применяться и для облачного случая.
Покажем, в заключение, что изложенные в этом разделе вычислительные алгоритмы действительно соответствуют решению уравнения переноса излучения (1.3.16).
Искомая характеристика излучения (интенсивность, поток) согласно выражениям интенсивности через функцию источников (1.3.21) и потока через интенсивность (1.1.4) может в операторной форме быть записана в виде
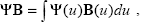 |
(2.1.20) |
где  (u) – некоторая функция, позволяющая по функции источников B(u) вычислить искомую величину (см., например, (1.3.21)). Переменная u здесь и далее вводится, чтобы не загромождать формулы, как абстрактная переменная интегрирования (вообще говоря, она соответствует интегрированию по координатам (u) – некоторая функция, позволяющая по функции источников B(u) вычислить искомую величину (см., например, (1.3.21)). Переменная u здесь и далее вводится, чтобы не загромождать формулы, как абстрактная переменная интегрирования (вообще говоря, она соответствует интегрированию по координатам  ', или (и) ', или (и)  ', ',  ' – см. (1.3.21), (1.1.4)). Функция источников, в свою очередь, определяется интегральным уравнением Фредгольма второго рода (1.3.23), (1.3.24) с ядром K и свободным членом q (1.3.24). ' – см. (1.3.21), (1.1.4)). Функция источников, в свою очередь, определяется интегральным уравнением Фредгольма второго рода (1.3.23), (1.3.24) с ядром K и свободным членом q (1.3.24).
Метод Монте-Карло изначально и был создан для вычисления интегралов вида (2.1.20):
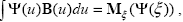 |
(2.1.21) |
где M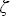 (…) – математическое ожидание случайной величины (…) – математическое ожидание случайной величины 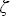 , которая моделируется по плотности вероятности B(u) (2.1.6). Таким образом, в методе Монте-Карло выражение (2.1.20), и уравнение для функции источников (1.3.23) записываются для одной траектории фотона, а искомая величина вычисляется по совокупности траекторий как математическое ожидание (2.1.21). Применяя (2.1.20) к формальному решению уравнения Фредгольма – ряду Неймана (1.3.25), получаем , которая моделируется по плотности вероятности B(u) (2.1.6). Таким образом, в методе Монте-Карло выражение (2.1.20), и уравнение для функции источников (1.3.23) записываются для одной траектории фотона, а искомая величина вычисляется по совокупности траекторий как математическое ожидание (2.1.21). Применяя (2.1.20) к формальному решению уравнения Фредгольма – ряду Неймана (1.3.25), получаем
 B = B =  q + q +  Kq + Kq +  K2q + K2q +  K3q + ... . K3q + ... . |
(2.1.22) |
Вычислительная схема метода Монте-Карло сводится к последовательному применению формулы (2.1.22): слагаемое  q –моделируется случайная величина q –моделируется случайная величина  (1), соответствующая плотности вероятности q, и записывается в счетчик значение (1), соответствующая плотности вероятности q, и записывается в счетчик значение  ( ( (1)); член (1)); член  Kq – моделируется случайная величина Kq – моделируется случайная величина  (2) по значению (2) по значению  (1) соответствующая плотности вероятности перехода K( (1) соответствующая плотности вероятности перехода K( (1), (1),  (2)) и записывается в счетчик значение (2)) и записывается в счетчик значение  ( ( (2)) и т.д.; общий член (2)) и т.д.; общий член  Knq – моделируется случайная величина Knq – моделируется случайная величина  (n+1) по значению (n+1) по значению  (n) соответствующая плотности вероятности перехода K( (n) соответствующая плотности вероятности перехода K( (n), (n),  (n+1)) и записывается в счетчик значение (n+1)) и записывается в счетчик значение  ( ( (n+1)). Траектория фотона в фазовом пространстве есть цепочка указанных переходов, моделирование производится по многим траекториям, искомая величина согласно формуле (2.1.22) – среднее значение (n+1)). Траектория фотона в фазовом пространстве есть цепочка указанных переходов, моделирование производится по многим траекториям, искомая величина согласно формуле (2.1.22) – среднее значение  ( ( ) по всем траекториям. ) по всем траекториям.
Теперь остается показать, что явный вид операторов q, K и  в описанных выше конкретных алгоритмах метода Монте-Карло соответствует их виду в формулах теории переноса, приведенных в разделе 1.3. При этом, поскольку в соотношения (1.3.23)‑(1.3.25) прямое излучение не включено, оператор Kq в нашем случае соответствует q из (1.3.24), (1.3.25), последнее для определенности обозначим q'. Фазовое пространство задается тремя координатами ( в описанных выше конкретных алгоритмах метода Монте-Карло соответствует их виду в формулах теории переноса, приведенных в разделе 1.3. При этом, поскольку в соотношения (1.3.23)‑(1.3.25) прямое излучение не включено, оператор Kq в нашем случае соответствует q из (1.3.24), (1.3.25), последнее для определенности обозначим q'. Фазовое пространство задается тремя координатами ( ', ', ', ', ') . Оператор q очевидно есть внеатмосферное излучение q=F0 ') . Оператор q очевидно есть внеатмосферное излучение q=F0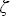 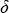 ( ( - -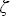 ) )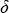 ( ( ), что соответствует оператору ), что соответствует оператору 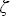 I0, рассмотренному в п.1.3 при получении соотношения (1.3.26). Следовательно, равенство q' = B I0, рассмотренному в п.1.3 при получении соотношения (1.3.26). Следовательно, равенство q' = B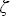 I0=Bq будет подтверждаться соответствием операторов K. I0=Bq будет подтверждаться соответствием операторов K.
Сначала рассмотрим случай без учета весов фотона w', т.е. будем явно моделировать поглощение излучения и положим формально w'  1 в локальных оценках (2.1.18) и (2.1.19). Как отмечено выше, оператор K описывает плотность вероятности перехода фотона между двумя точками фазового пространства, координаты которых, для согласования с определениями (1.3.24) обозначим как ( 1 в локальных оценках (2.1.18) и (2.1.19). Как отмечено выше, оператор K описывает плотность вероятности перехода фотона между двумя точками фазового пространства, координаты которых, для согласования с определениями (1.3.24) обозначим как ( ', ', ', ', ')и ( ')и ( , , , , ). Плотность вероятности K по смыслу есть произведение трех плотностей вероятности: пробега фотоном расстояния ). Плотность вероятности K по смыслу есть произведение трех плотностей вероятности: пробега фотоном расстояния 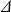  '= '= - - ' (2.1.8), непоглощения его в атмосфере , рассеяния с изменением направления с ( ' (2.1.8), непоглощения его в атмосфере , рассеяния с изменением направления с ( ', ', ') на ( ') на ( , , ), равной по формуле (2.1.19) x( ), равной по формуле (2.1.19) x( , ,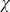 ')/(4 ')/(4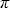 ). Но это произведение в точности равно K согласно соотношениям (1.3.24)! Заметим, что для учета в методе Монте-Карло влияния подстилающей поверхности, принимая во внимание, что по формулам (2.1.6), (2.1.11) вероятность отражения фотона в интервале направлений [- ). Но это произведение в точности равно K согласно соотношениям (1.3.24)! Заметим, что для учета в методе Монте-Карло влияния подстилающей поверхности, принимая во внимание, что по формулам (2.1.6), (2.1.11) вероятность отражения фотона в интервале направлений [- ',0] равна P( ',0] равна P( ')= 2 arccos(- ')= 2 arccos(-  ')/ ')/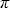 , к выражениям (1.3.24) добавляется следующее условие: , к выражениям (1.3.24) добавляется следующее условие:
при  '= '= 0, 0,  ' <0 ' <0
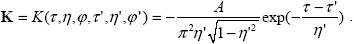 . . |
(2.1.23) |
Теперь, для нахождения оператора  , учтем, что переменные, обозначенные в определении оператора K по формуле (1.3.24) как ( , учтем, что переменные, обозначенные в определении оператора K по формуле (1.3.24) как ( , , , , ), далее при вычислении искомых величин по (2.1.20) сами становятся переменными интегрирования. Например, при вычислении интенсивности по функции источника (1.3.21) ), далее при вычислении искомых величин по (2.1.20) сами становятся переменными интегрирования. Например, при вычислении интенсивности по функции источника (1.3.21)  ' – это переменная, обозначенная в уравнениях для функции источника (1.3.22)‑(1.3.24) как ' – это переменная, обозначенная в уравнениях для функции источника (1.3.22)‑(1.3.24) как  . Поэтому координаты точки ( . Поэтому координаты точки ( , , , , ) теперь следует обозначить в (2.1.10) уже как ( ) теперь следует обозначить в (2.1.10) уже как ( ', ', ', ', '). После вычисления интенсивности излучения по формуле (1.3.21) поток вычисляется через нее исходя из соотношения (1.1.4), при этом множитель сокращается, интегрирование производится по всем трем переменным ( '). После вычисления интенсивности излучения по формуле (1.3.21) поток вычисляется через нее исходя из соотношения (1.1.4), при этом множитель сокращается, интегрирование производится по всем трем переменным ( ', ', ', ', '), что из соотношений (1.3.21) и (1.1.4) дает для величины '), что из соотношений (1.3.21) и (1.1.4) дает для величины  выражение, в точности совпадающее с простой локальной оценкой (2.1.18). При вычислении же интенсивности по формуле (1.3.21) переменной интегрирования является только выражение, в точности совпадающее с простой локальной оценкой (2.1.18). При вычислении же интенсивности по формуле (1.3.21) переменной интегрирования является только  ', зависимость функции источников B от координат ( ', зависимость функции источников B от координат ( ', ', ') отсутствует. Действительно, плотность вероятности перехода K записана, с учетом смены обозначений, для координат ( ') отсутствует. Действительно, плотность вероятности перехода K записана, с учетом смены обозначений, для координат ( ', ', ', ', '), а при вычислении интенсивности по формулам (1.3.21) используются координаты ( '), а при вычислении интенсивности по формулам (1.3.21) используются координаты ( , , , , ). Следовательно, угол рассеяния, по которому моделировалась траектория фотона в операторе K в методе Монте-Карло (2.1.22), не тот, что стоит в операторе (1.3.24) уравнения переноса. Поэтому соответствующая нужному углу ( ). Следовательно, угол рассеяния, по которому моделировалась траектория фотона в операторе K в методе Монте-Карло (2.1.22), не тот, что стоит в операторе (1.3.24) уравнения переноса. Поэтому соответствующая нужному углу ( ', ', ') плотность вероятности рассеяния еще не учтена. Ее учету и соответствует умножение на индикатрису рассеяния в выражении для локальной оценки (2.1.19). Таким образом, и при рассмотрении интенсивности излучения мы получаем полное соответствие формул (2.1.19) и (1.3.21) ‑ (1.3.24). ') плотность вероятности рассеяния еще не учтена. Ее учету и соответствует умножение на индикатрису рассеяния в выражении для локальной оценки (2.1.19). Таким образом, и при рассмотрении интенсивности излучения мы получаем полное соответствие формул (2.1.19) и (1.3.21) ‑ (1.3.24).
Случай моделирования траектории фотона с учетом весов w' соответствует согласованному видоизменению операторов K и  , учитывая, что они входят в решение (2.1.22) только в виде свертки , учитывая, что они входят в решение (2.1.22) только в виде свертки  K. В этом случае операция умножения на вероятность выживания кванта K. В этом случае операция умножения на вероятность выживания кванта  0( 0( ) переносится из оператора K в оператор ) переносится из оператора K в оператор  , что при вычислении степеней оператора K в формуле (2.1.22) как раз и соответствует изменению веса фотона w' и умножению на эту величину соответствующих локальных оценок в формулах (2.1.18), (2.1.19) . Аналогично приходим к выводу о том, что прямое моделирование потоков излучения наоборот соответствует переходу экспоненциального множителя из выражения для локальной оценки (2.1.18) в оператор K. На подобных преобразованиях, многие из которых сложно изложить с точки зрения физического моделирования, базируются многие другие разнообразные приемы оптимизации вычислений в методе Монте-Карло , , в частности вычисление производных от потоков излучения, которое мы рассмотрим в гл.5. С помощью этих методов, как показано выше, реально решается одно и то же уравнение переноса (1.3.16), но с разными вариантами записи конкретных “решающих операторов” K и , что при вычислении степеней оператора K в формуле (2.1.22) как раз и соответствует изменению веса фотона w' и умножению на эту величину соответствующих локальных оценок в формулах (2.1.18), (2.1.19) . Аналогично приходим к выводу о том, что прямое моделирование потоков излучения наоборот соответствует переходу экспоненциального множителя из выражения для локальной оценки (2.1.18) в оператор K. На подобных преобразованиях, многие из которых сложно изложить с точки зрения физического моделирования, базируются многие другие разнообразные приемы оптимизации вычислений в методе Монте-Карло , , в частности вычисление производных от потоков излучения, которое мы рассмотрим в гл.5. С помощью этих методов, как показано выше, реально решается одно и то же уравнение переноса (1.3.16), но с разными вариантами записи конкретных “решающих операторов” K и  . На практике удобно пользоваться следующим приемом: считать, что плотность вероятности перехода K всегда определяется конкретной схемой моделирования траекторий фотонов, а оператор . На практике удобно пользоваться следующим приемом: считать, что плотность вероятности перехода K всегда определяется конкретной схемой моделирования траекторий фотонов, а оператор  – конкретной записью в счетчики (иначе говоря, K “отвечает” за перенос излучения, а – конкретной записью в счетчики (иначе говоря, K “отвечает” за перенос излучения, а  – за модель его “измерения”). – за модель его “измерения”). |